Aplicaciones del método de abatimiento por la recta frontal

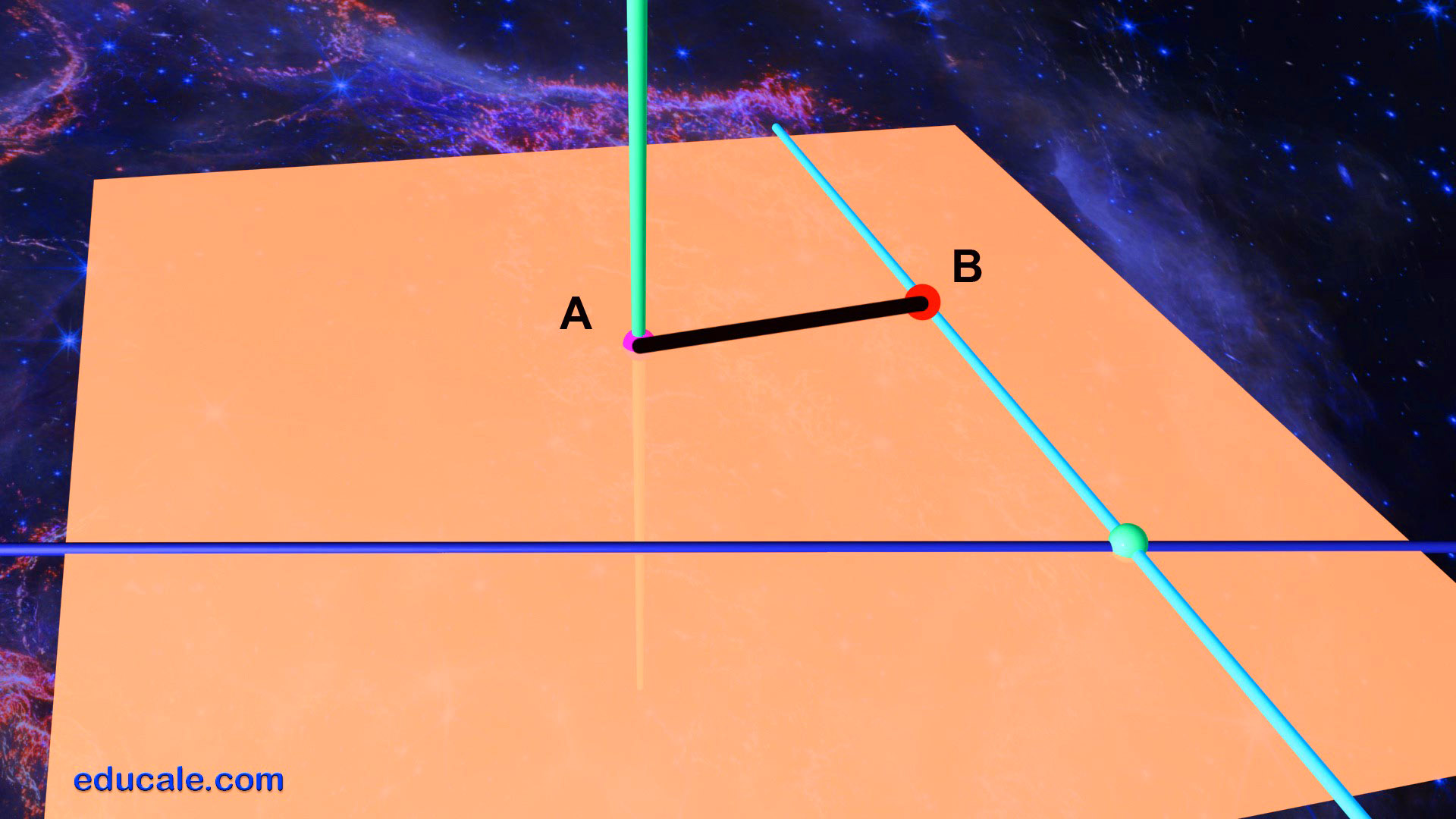
1 - Nuevo procedimiento para hallar la perpendicular común entre dos rectas que se cruzan

Se elige un punto cualquiera, y por él se hace pasar una recta frontal y perpendicular a la otra recta dada. Sabiendo que la perpendicularidad entre rectas, en el sistema diédrico, es directa, utilizando rectas frontales u horizontales. Se hallan las trazas del plano que forman estas dos rectas que se cortan.
Se localiza el punto de intersección de la otra recta con el plano hallado.
Abatimos este punto de intersección y la otra recta, mediante el método de abatimiento de la recta frontal.
Ya en verdadera magnitud, trazamos el segmento mínima distancia perpendicularmente desde el punto de intersección hasta la recta

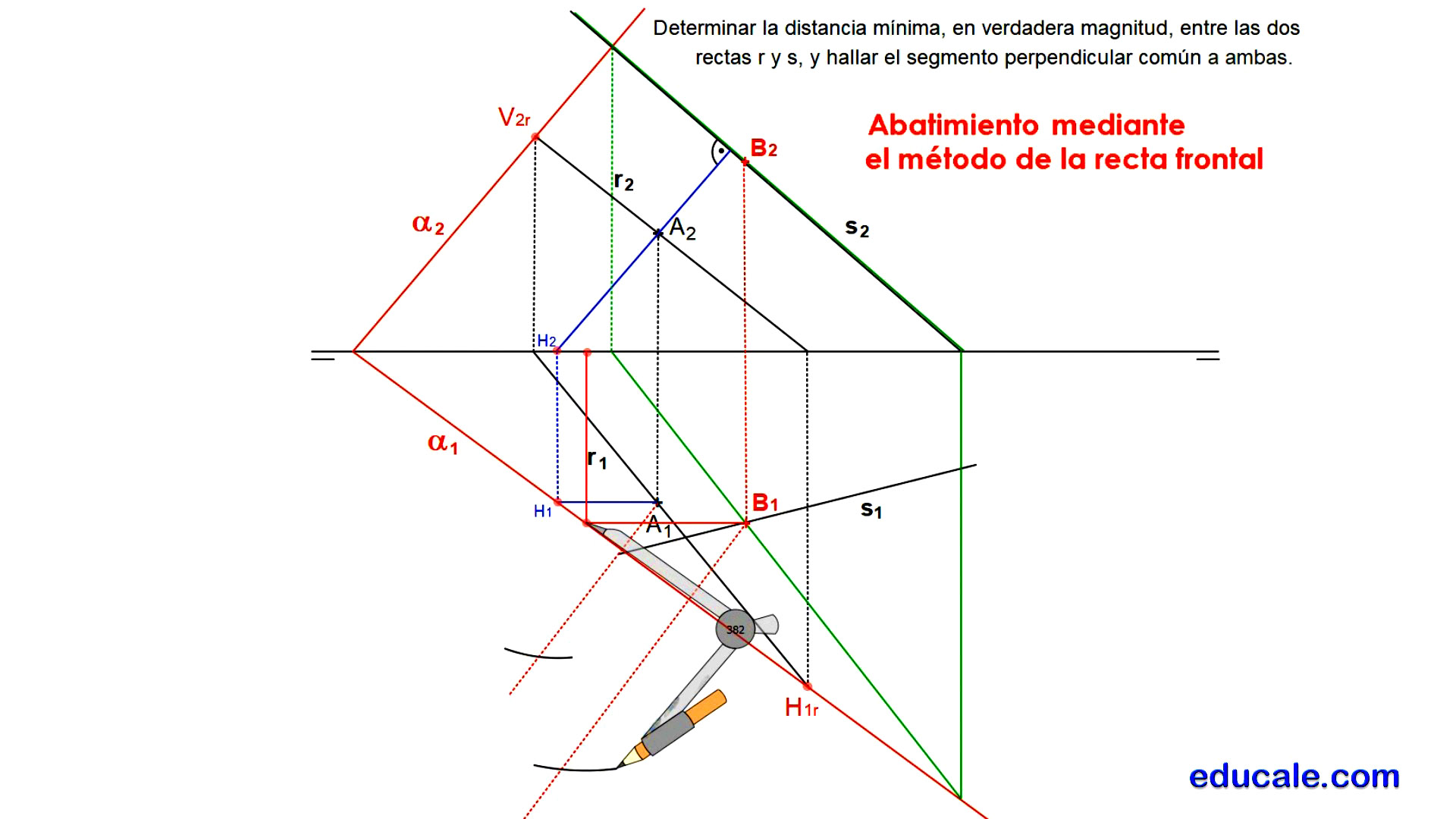
2 - Hallar la distancia mínima y la perpendicular común entre dos rectas que se cruzan por el nuevo procedimiento

Se elige un punto cualquiera A, y por él se hace pasar una recta frontal y perpendicular a la otra recta dada. Sabiendo que la perpendicularidad entre rectas, en el sistema diédrico, es directa, utilizando rectas frontales u horizontales. Se hallan las trazas del plano que forman estas dos rectas que se cortan.

Se localiza el punto de intersección B de la otra recta con el plano hallado.
Abatimos los puntos A y B, mediante el método de abatimiento de la recta frontal.
Unimos el punto A, abatido, con la traza horizontal de su recta para dibujar la recta r abatida.
Ya en verdadera magnitud, trazamos el segmento mínima distancia, con un ángulo de 90º desde el punto de intersección B, hasta la recta r.
Dibujamos una perpendicular a la traza horizontal del plano, para localizar sobre s1 la proyección horizontal del punto B.
Y, perpendicularmente a la línea de tierra, se halla B2 sobre la proyección vertical de la recta s.