Aplicaciones del método de abatimiento por la recta frontal

7 - Ángulo entre recta y plano

7.1 - Procedimiento para hallar el ángulo que forma una recta con un plano

Elegimos un punto cualquiera A de la recta dada.
Por este punto, pasamos una recta perpendicular al plano, sabiendo que la perpendicularidad entre rectas y planos es directa.
Hallamos las trazas horizontales de estas dos rectas.
Uniendo estas trazas, dibujamos la traza horizontal del plano que las contiene.
Se abate el punto A mediante el método de abatimiento de la recta frontal del plano.
Unimos el punto A abatido, con las trazas horizontales de las rectas que forman este plano, para dibujar estas rectas abatidas.
Ya en abatido, por cualquier parte de la recta perpendicular al plano, se dibuja un segmento perpendicular a ella, trazando un triángulo rectángulo.
El ángulo que forma la recta con el plano, es el ángulo agudo opuesto al punto A abatido de este triángulo.

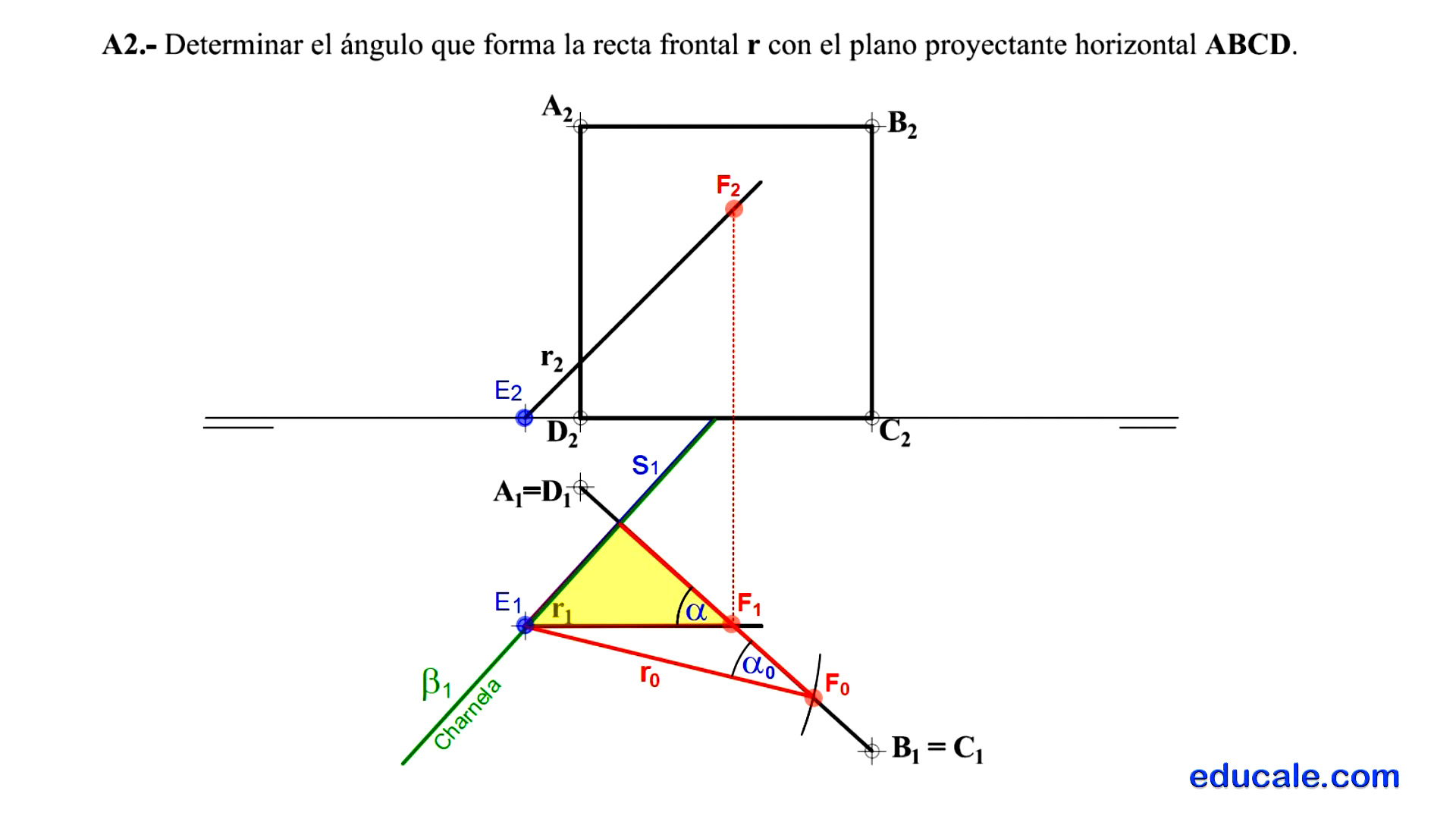
7.2 - Hallar el ángulo en verdadera magnitud que forma la recta r con el plano ABCD

Elegimos un punto cualquiera E de la recta dada.
Por este punto, pasamos una recta perpendicular al plano, sabiendo que la perpendicularidad entre rectas y planos es directa.
La traza horizontal del plano, que contiene las rectas r y s, es la propia proyección s1.
La recta r es una recta frontal del plano y su traza horizontal es E1.
Se localiza un punto cualquiera F de esta recta r.
Se abate este punto mediante el método de abatimiento de la recta frontal del plano.
Unimos el punto F abatido, con su traza horizontal E1 para dibujar esta recta abatida.
Al ser el plano dado, un plano proyectante horizontal, el triángulo rectángulo solución ya estará formado.
El ángulo que forma la recta con el plano, es el ángulo agudo opuesto al punto E abatido (E1).

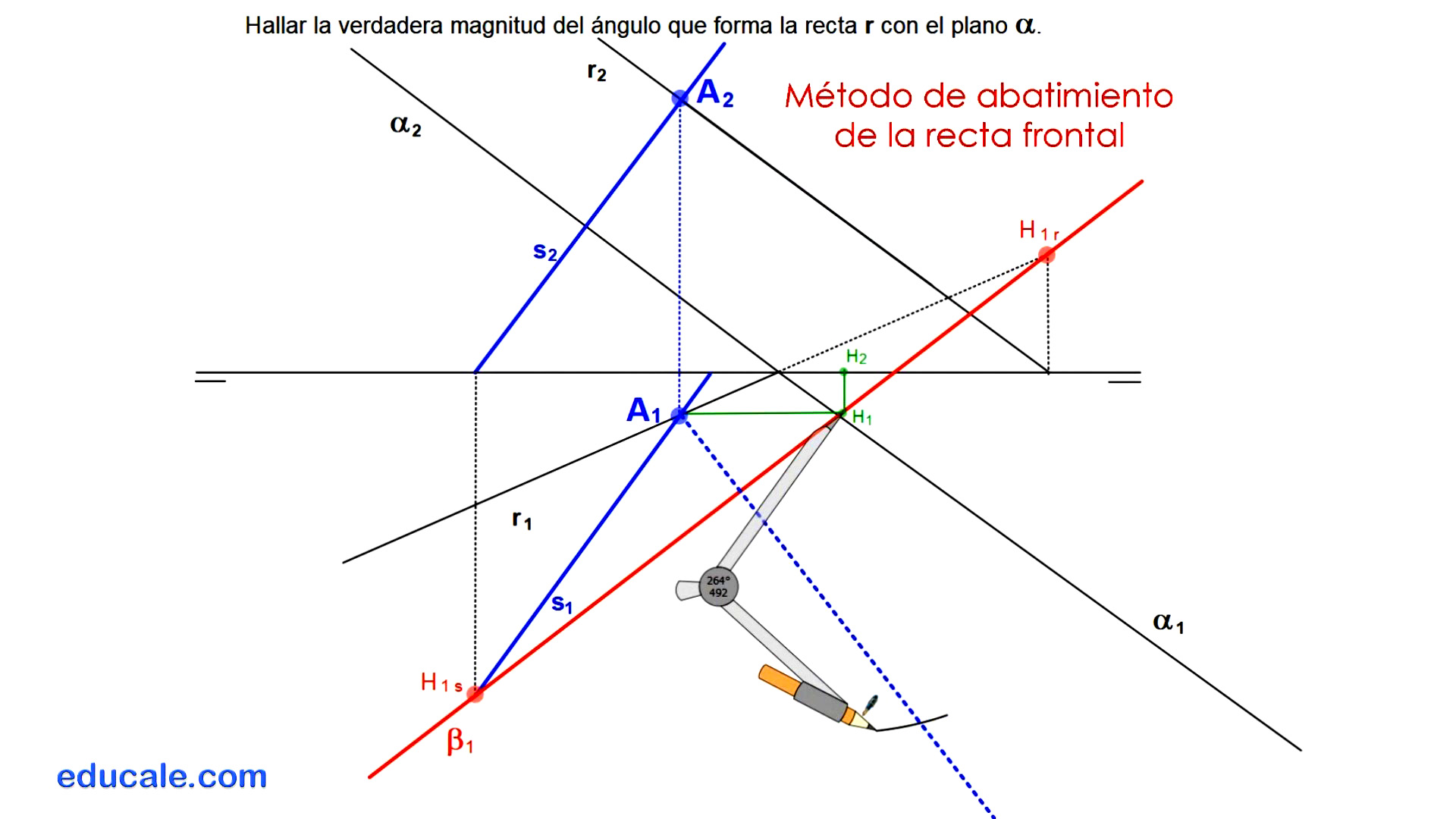
7.3 - Ángulo en verdadera magnitud entre recta y plano proyectante vertical

Elegimos un punto cualquiera A de la recta dada.
Por este punto, pasamos una recta s perpendicular al plano, sabiendo que la perpendicularidad entre rectas y planos es directa.
Hallamos las trazas horizontales de estas dos rectas.
Uniendo estas trazas, dibujamos la traza horizontal del plano que las contiene.
La recta s es una recta frontal del plano
Se abate el punto A mediante el método de abatimiento de la recta frontal del plano.
Unimos el punto A abatido, con las trazas horizontales de las rectas que forman este plano, para dibujar estas rectas abatidas.
Ya en abatido, por cualquier parte de la recta s perpendicular al plano, se dibuja un segmento perpendicular a ella, trazando un triángulo rectángulo solución.
El ángulo que forma la recta con el plano, es el ángulo agudo opuesto al punto A abatido de este triángulo.

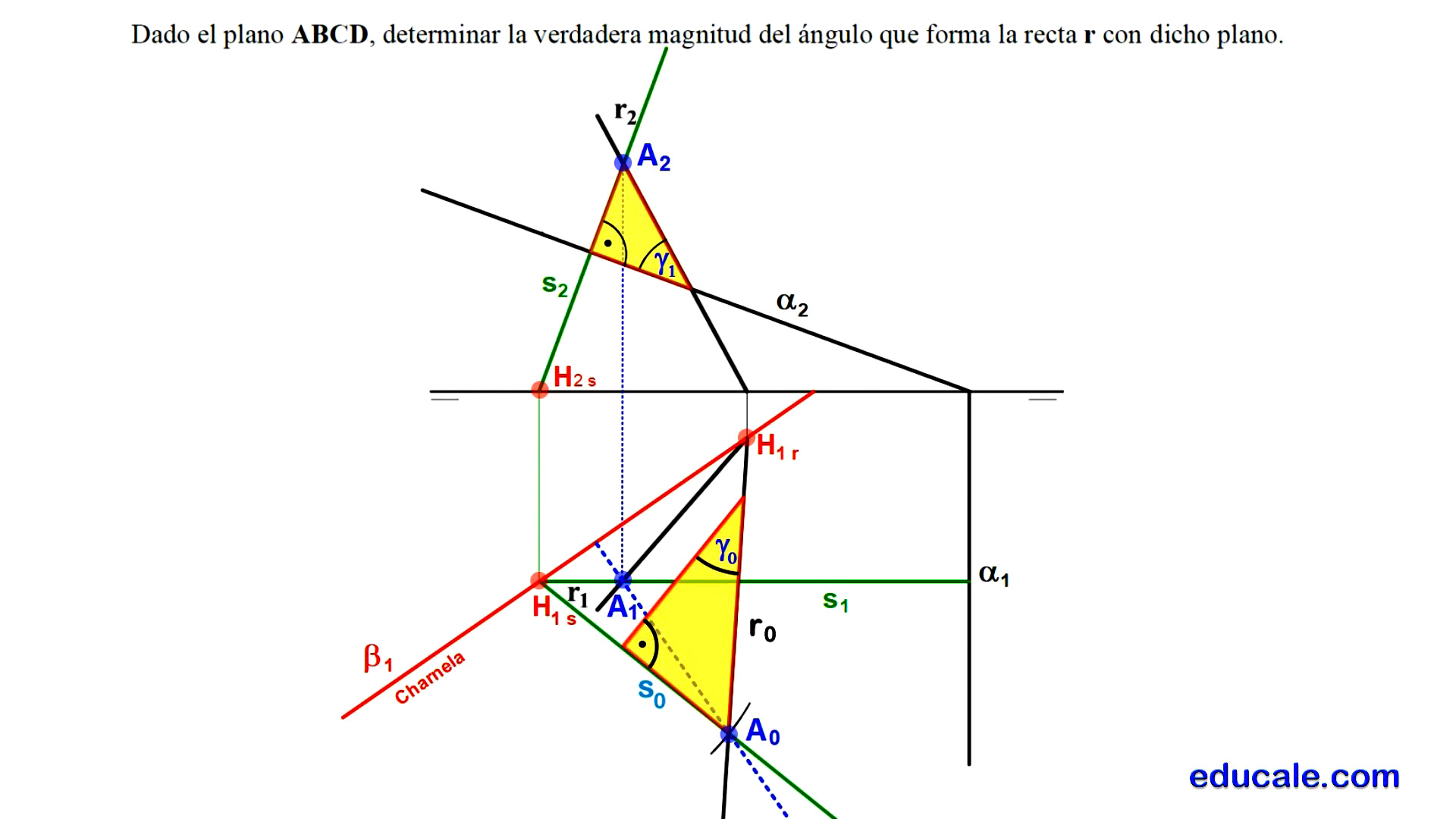
7.4 - Hallar la verdadera magnitud del ángulo que forma la recta r con el plano

Elegimos un punto cualquiera A de la recta dada.
Por este punto, pasamos una recta s perpendicular al plano, sabiendo que la perpendicularidad entre rectas y planos es directa.
Hallamos las trazas horizontales de estas dos rectas.
Uniendo estas trazas, dibujamos la traza horizontal del plano que las contiene.
Por el punto A, dibujamos la recta frontal del plano, localizando su traza horizontal.
Se abate este punto mediante el método de abatimiento de la recta frontal del plano.
Unimos el punto A abatido, con las trazas horizontales de las rectas que forman este plano, para dibujar estas rectas abatidas.
Ya en abatido, por cualquier parte de la recta s perpendicular al plano, se dibuja un segmento perpendicular a ella, trazando un triángulo rectángulo solución.
El ángulo que forma la recta con el plano, es el ángulo agudo opuesto al punto A abatido de este triángulo.

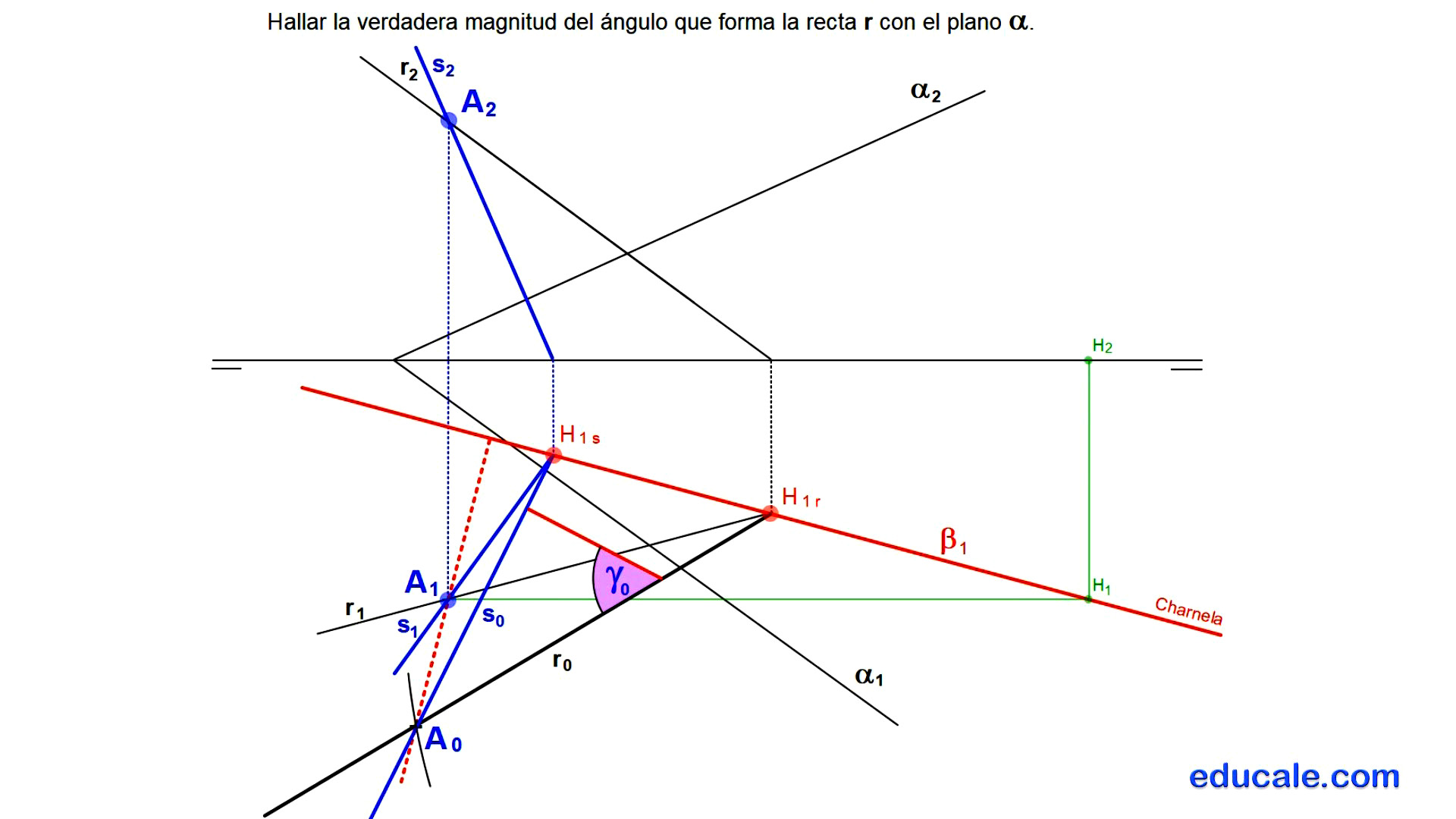
7.5 - Hallar la verdadera magnitud del ángulo que forma la recta r con el plano

Elegimos un punto cualquiera A de la recta dada.
Por este punto, pasamos una recta s perpendicular al plano, sabiendo que la perpendicularidad entre rectas y planos es directa.
Hallamos las trazas horizontales de estas dos rectas.
Uniendo estas trazas, dibujamos la traza horizontal del plano que las contiene.
Por el punto A, dibujamos la recta frontal del plano, localizando su traza horizontal.
Se abate este punto mediante el método de abatimiento de la recta frontal del plano.
Unimos el punto A abatido, con las trazas horizontales de las rectas que forman este plano, para dibujar estas rectas abatidas.
Ya en abatido, por cualquier parte de la recta s perpendicular al plano, se dibuja un segmento perpendicular a ella, trazando un triángulo rectángulo solución.
El ángulo que forma la recta con el plano, es el ángulo agudo opuesto al punto A abatido de este triángulo.