Aplicaciones del método de abatimiento por la recta frontal

8 - Ángulo entre dos rectas

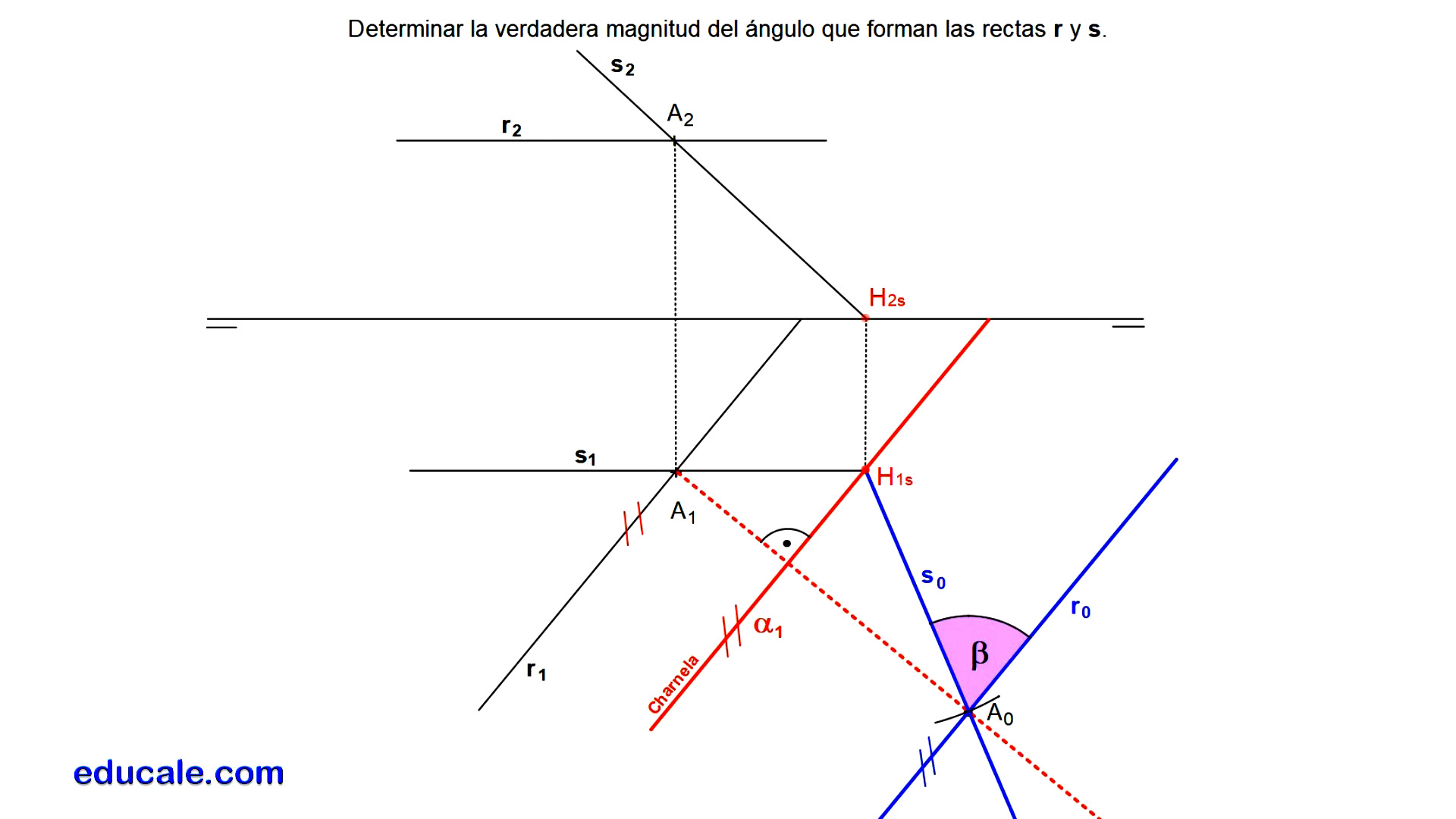
8.1 - Determinar el ángulo en verdadera magnitud entre una recta frontal y otra horizontal

Estas dos rectas se cortan en el punto A.
Encontramos las trazas horizontales de estas dos rectas. Sin embargo, la recta r, al ser una recta horizontal, tiene su traza en el infinito. Por lo tanto, no tiene, pero sí nos determina la dirección, que será paralela a su traza horizontal.
Por la traza horizontal de la recta s y paralela a la dirección de r1, dibujamos la traza horizontal del plano que las contiene.
Se abate el punto A mediante el método de abatimiento de la recta frontal del plano.
Unimos el punto A abatido con la traza horizontal de la recta s, para dibujar esta recta abatida. La recta r abatida pasará también por el punto A abatido y será paralela a la charnela o a r1.
Una vez abatidas las rectas, se señala el ángulo en verdadera magnitud, sabiendo que el ángulo será siempre el de menor tamaño o menor de 90º.

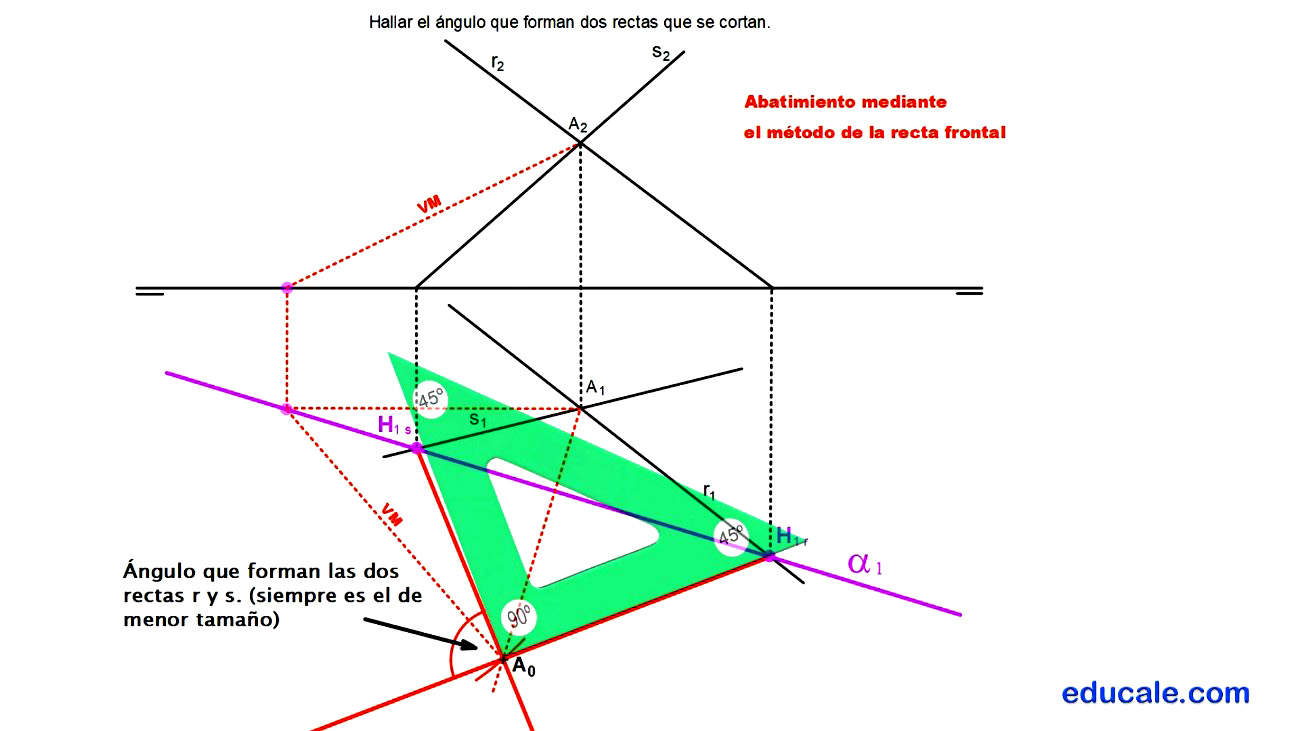
8.2 - Hallar el ángulo que forman dos rectas que se cortan

Hallamos las trazas horizontales de estas dos rectas.
Uniendo estas trazas, dibujamos la traza horizontal del plano que las contiene.
Por el punto A, dibujamos la recta frontal del plano, localizando su traza horizontal.
Se abate el punto A mediante el método de abatimiento de la recta frontal del plano.
Unimos el punto A abatido, con las trazas horizontales de las rectas que forman este plano, para dibujar estas rectas abatidas.
Una vez abatidas las rectas, se señala el ángulo en verdadera magnitud, sabiendo que el ángulo será siempre el de menor tamaño o menor de 90º.

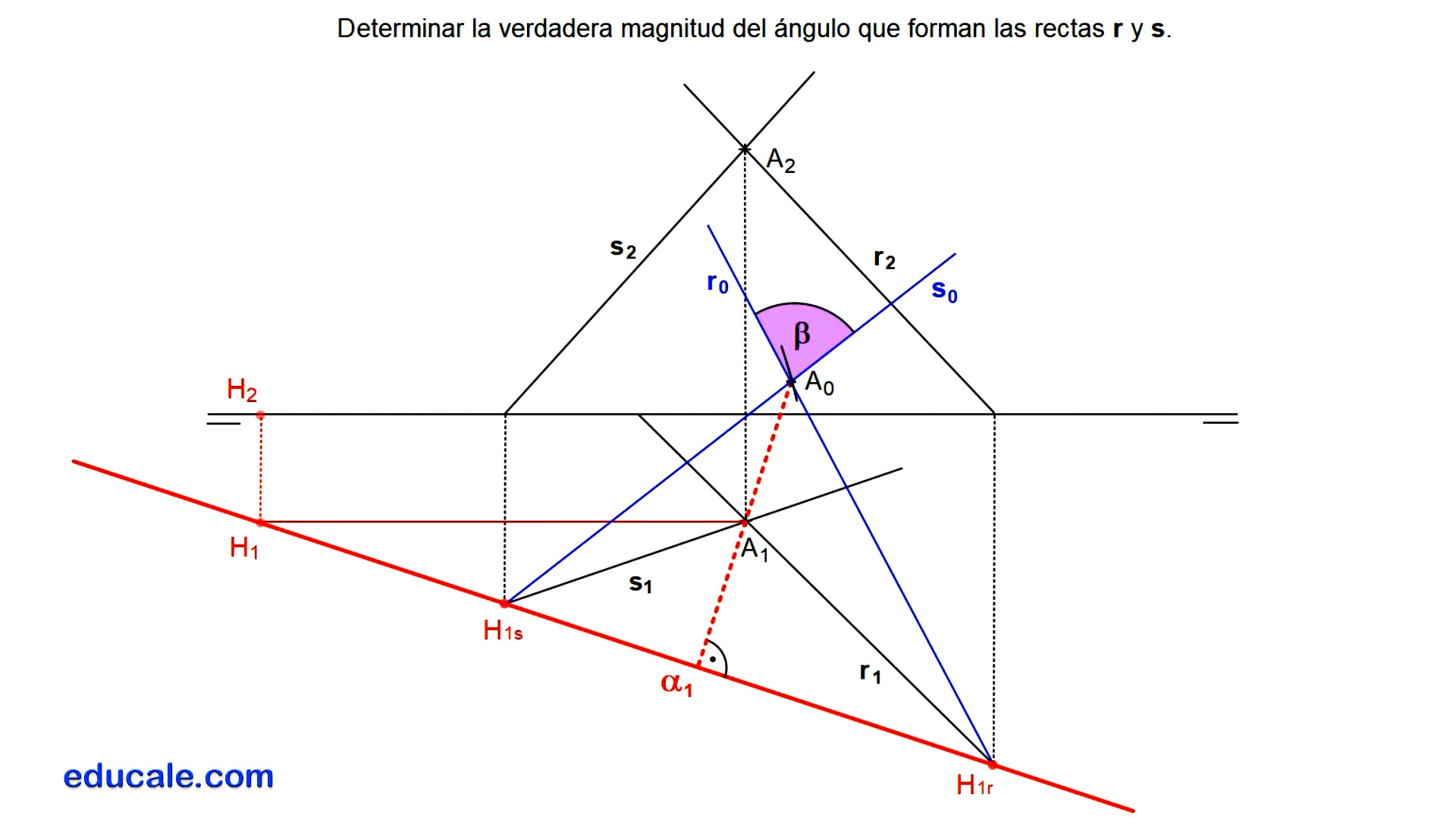
8.3 - Determinar el ángulo en verdadera magnitud entre dos recta

Localizamos las trazas horizontales de estas dos rectas.
Uniendo estas trazas, dibujamos la traza horizontal del plano que las contiene.
Por el punto A, dibujamos la recta frontal del plano, localizando su traza horizontal.
Se abate el punto A mediante el método de abatimiento de la recta frontal del plano.
Unimos el punto A abatido, con las trazas horizontales de las rectas que forman este plano, para dibujar estas rectas abatidas.
Una vez abatidas las rectas, se señala el ángulo en verdadera magnitud, sabiendo que el ángulo será siempre el de menor tamaño o menor de 90º.

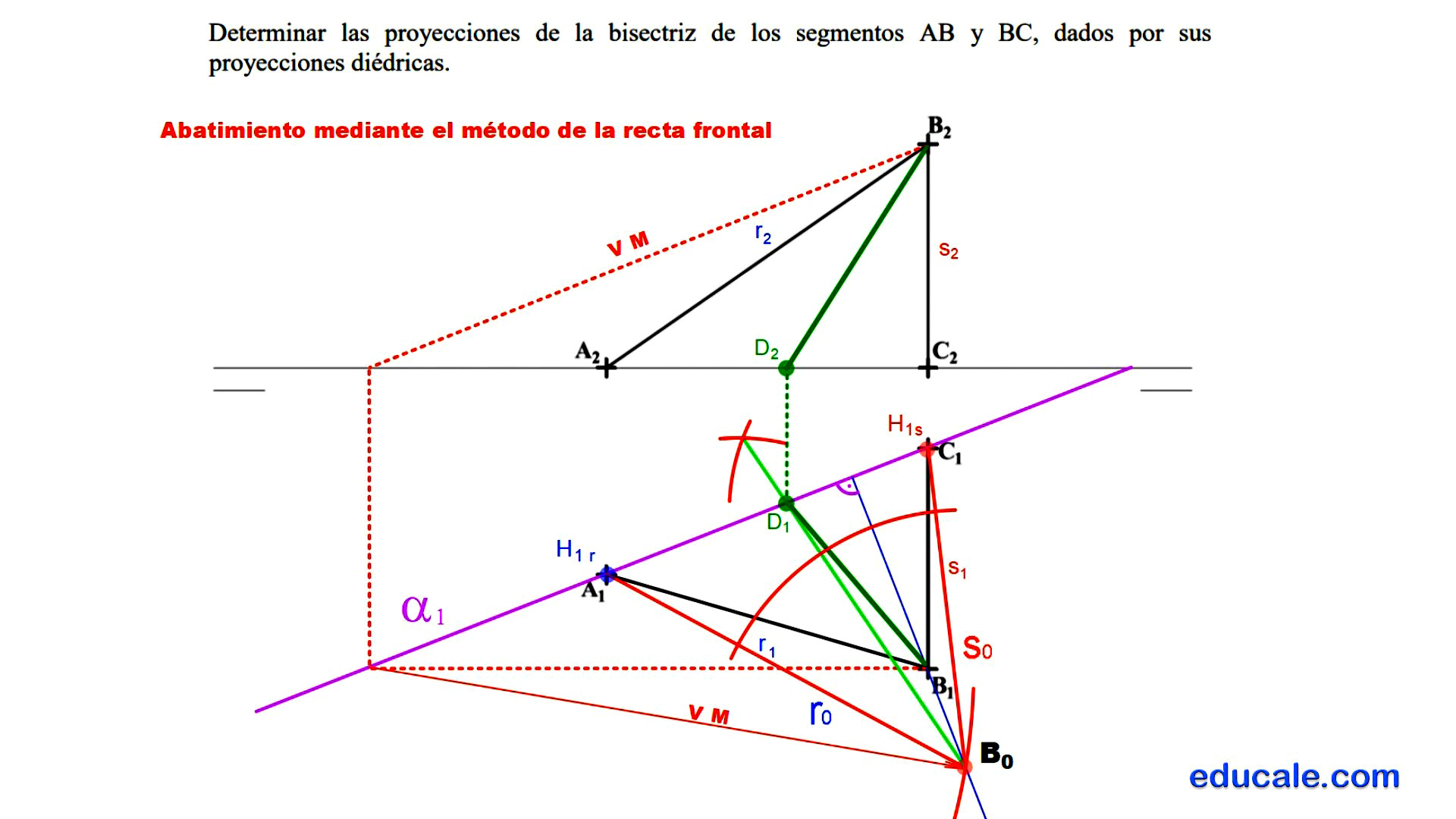
8.4 - Determinar las proyecciones de la bisectriz de los segmentos AB y BC

Las proyecciones horizontales de los puntos A y C coinciden con las trazas horizontales de las rectas que los contienen.
Uniendo estas proyecciones, dibujamos la traza horizontal del plano que las contiene.
Por el punto B, dibujamos la recta frontal del plano, localizando su traza horizontal.
Se abate el punto B mediante el método de abatimiento de la recta frontal del plano.
Unimos el punto B abatido, con las trazas horizontales de las rectas que forman este plano, para dibujar estas rectas abatidas.
Una vez abatidas las rectas, se dibuja la bisectriz del ángulo que forman. Esta bisectriz nos genera un punto D en la traza horizontal del plano. Localizamos la proyección vertical de D sobre la línea de tierra, que denominaremos D2.
Unimos las proyecciones de los puntos B y D para representar la bisectriz requerida.

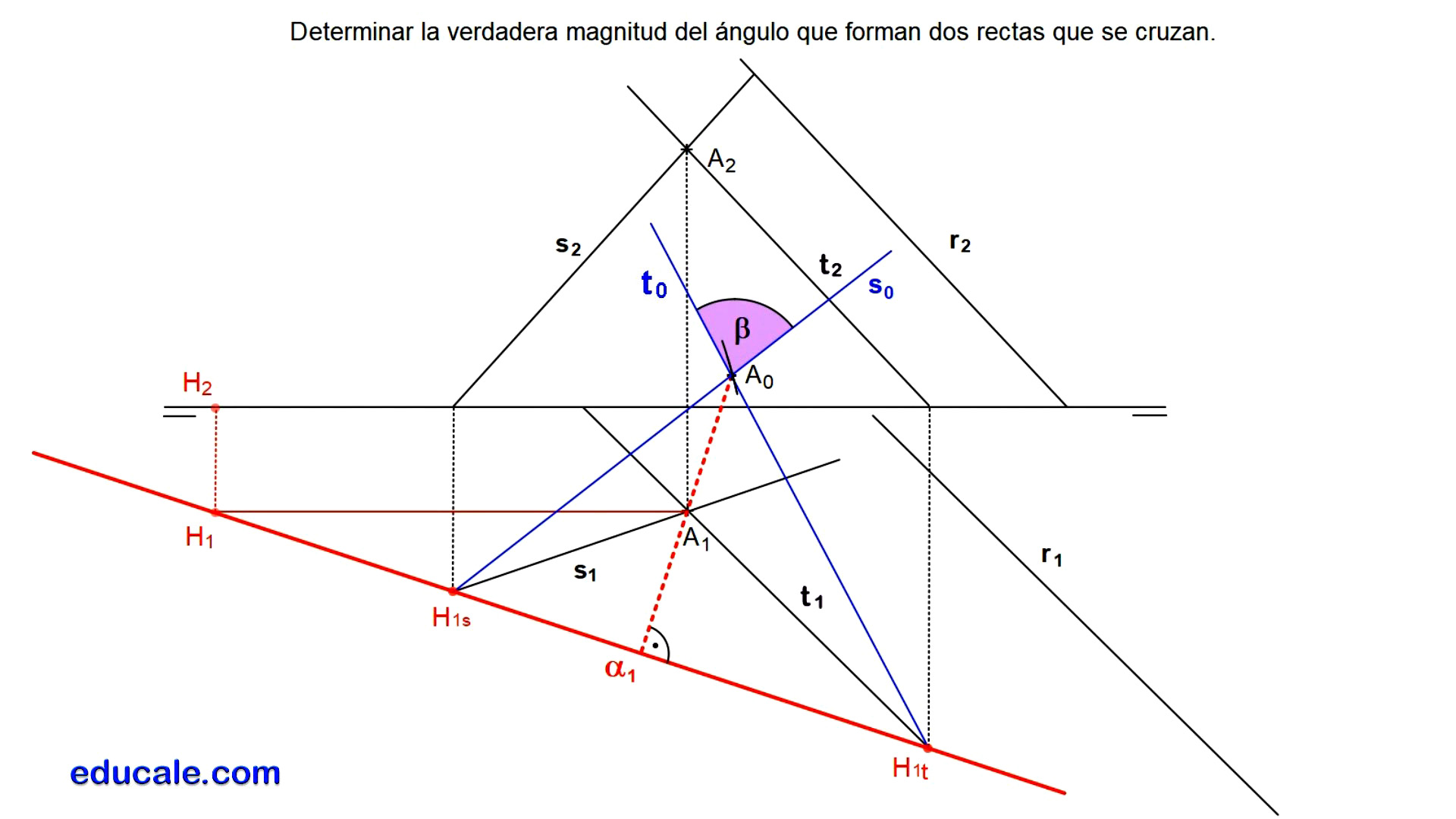
8.5 - Determinar la verdadera magnitud del ángulo que forman dos rectas que se cruzan

Elegimos un punto cualquiera A en una de las dos rectas.
Por este punto se dibuja una recta paralela a la otra recta dada.
Ahora hemos transformado el ejercicio en determinar la verdadera magnitud del ángulo que forman dos rectas que se cortan.
Localizamos las trazas horizontales de estas dos rectas.
Uniendo estas trazas, dibujamos la traza horizontal del plano que las contiene.
Por el punto A, dibujamos la recta frontal del plano, localizando su traza horizontal.
Se abate el punto A mediante el método de abatimiento de la recta frontal del plano.
Unimos el punto A abatido, con las trazas horizontales de las rectas que forman este plano, para dibujar estas rectas abatidas.
Una vez abatidas las rectas, se señala el ángulo en verdadera magnitud, sabiendo que el ángulo será siempre el de menor tamaño o menor de 90º.