10 - Otros nuevos métodos de abatimientos

10.1 - Cuatro casos de Abatimientos de rectas

1.er caso:
Hallamos las trazas de la recta.
Con centro en V1 y radio hasta H1, se traza un arco de circunferencia hasta la línea de tierra, obteniendo la traza horizontal de la recta abatida H0 sobre el plano vertical de proyección.
Uniendo H0 con V2 obtendremos la recta abatida sobre el plano vertical de proyección.

2º caso:
Hallamos las trazas de la recta. En este caso la traza horizontal se encuentra entre cuadrantes ocultos.
Con centro en V1 y radio hasta H1, se traza un arco de circunferencia hasta la línea de tierra, obteniendo la traza horizontal de la recta abatida H0 sobre el plano vertical de proyección.
Uniendo H0 con V2 obtendremos la recta abatida sobre el plano vertical de proyección.

3.er caso:
Hallamos las trazas de la recta. En este caso la traza vertical se encuentra entre cuadrantes ocultos.
Con centro en V1 y radio hasta H1, se traza un arco de circunferencia hasta la línea de tierra, obteniendo la traza horizontal de la recta abatida H0 sobre el plano vertical de proyección.
Uniendo H0 con V2 obtendremos la recta abatida sobre el plano vertical de proyección.

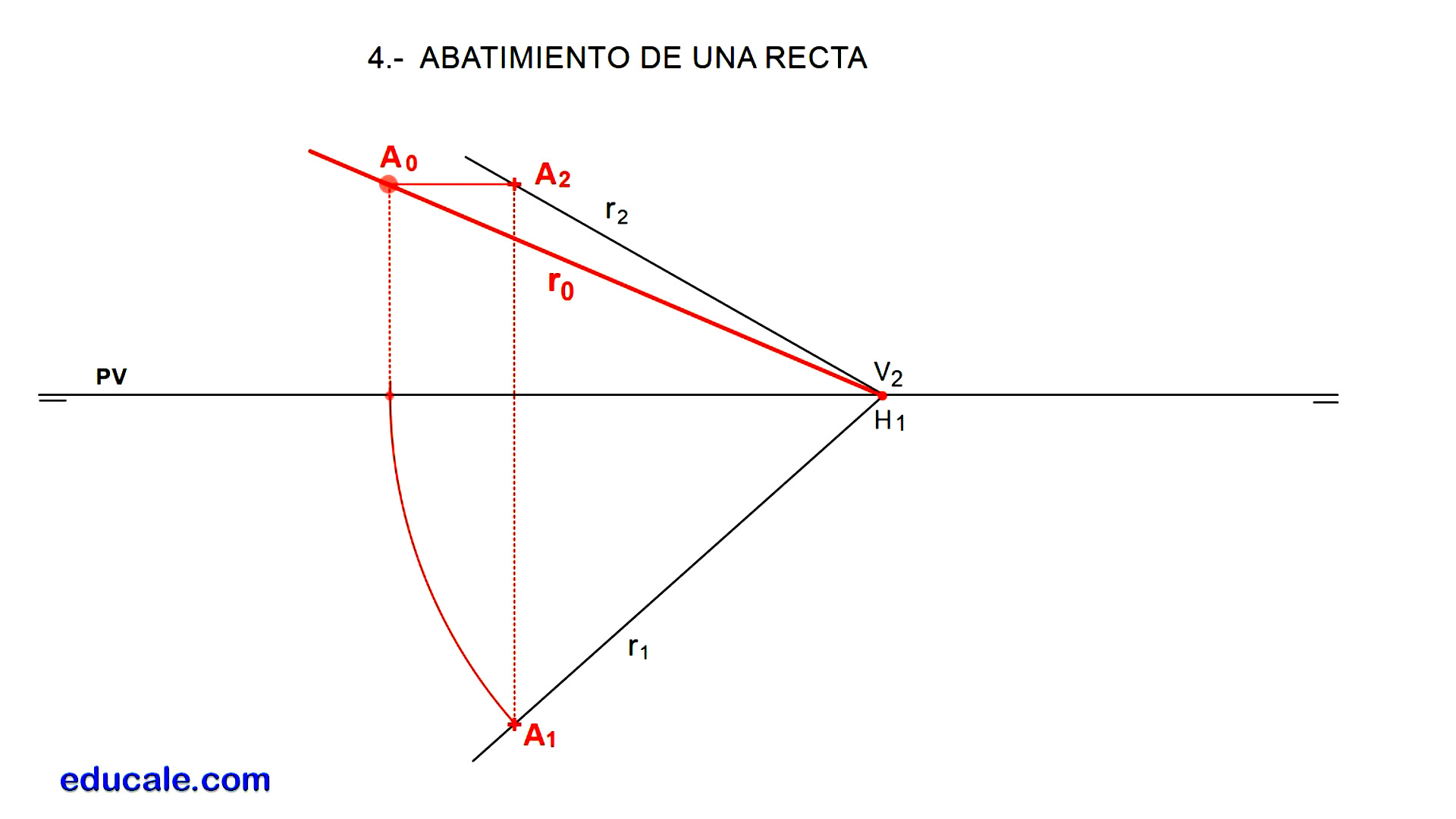
4º caso:
Hallamos las trazas de la recta. En este caso las dos trazas coinciden en la línea de tierra.
Elegimos un punto cualquiera A en la recta.
Con centro en H1 y radio igual a A1, se traza un arco de circunferencia hasta la línea de tierra. Desde el punto de intersección del arco con la línea de tierra, se traza una perpendicular hasta la altura del punto A, obteniendo así la posición del punto A abatido sobre el plano vertical de proyección.
Uniendo A0 con V2 obtendremos la recta abatida sobre el plano vertical de proyección.

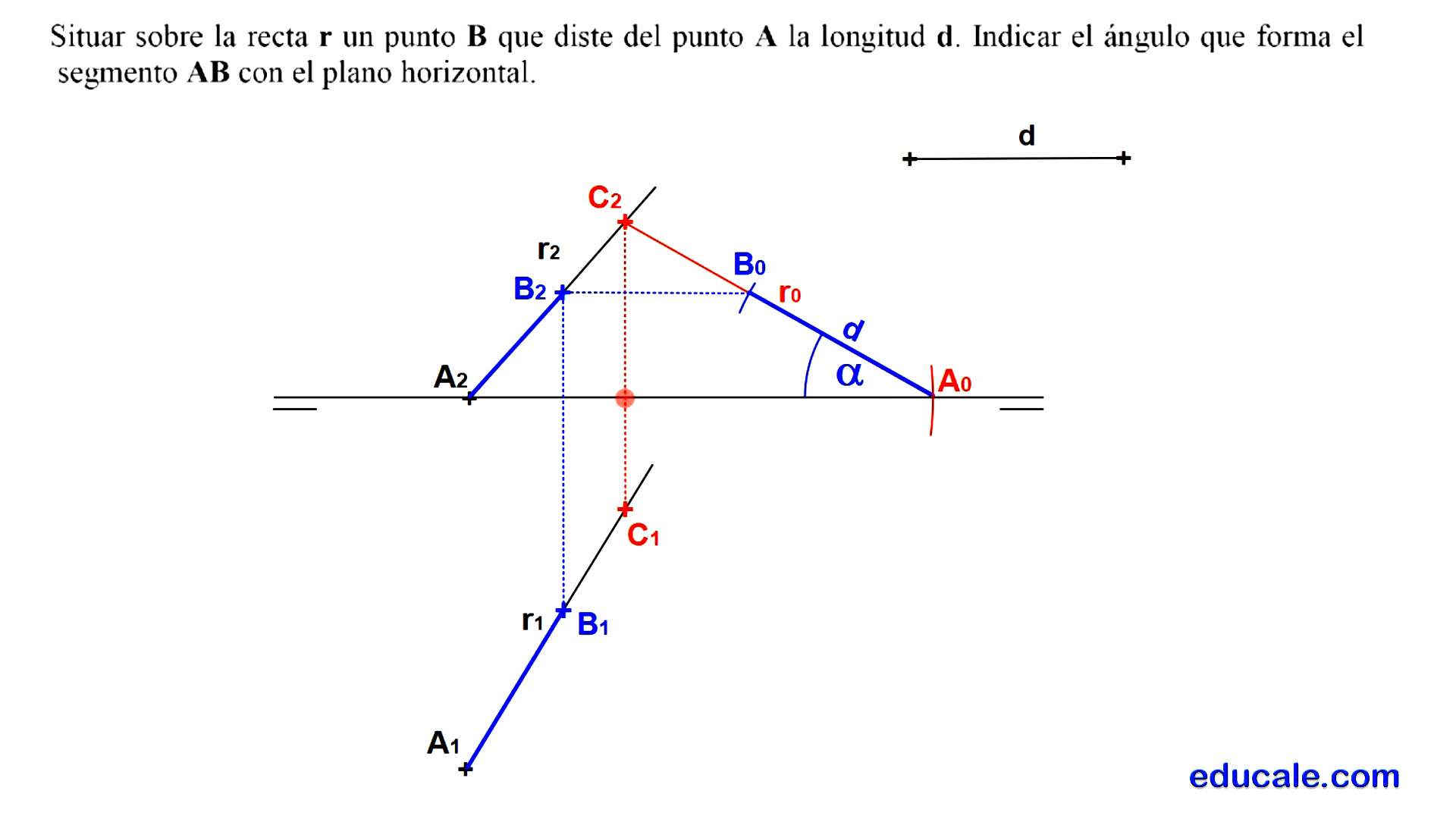
10.2 - Situar un segmento de longitud d sobre una recta indicar el ángulo con el plano horizontal

Elegimos un punto cualquiera C en la recta.
Con radio desde C1 hasta A1, y centro en el punto de intersección de la proyección de C con la línea de tierra, trazaremos un arco que nos determinará la posición del punto A abatido sobre el plano vertical de proyección.
Uniendo A0 con C2 obtendremos la recta abatida sobre el plano vertical de proyección.
Sobre esta recta y desde A0 llevamos la medida del segmento d, obteniendo B0.
Para determinar la proyección vertical del punto B sobre r2, trazamos una línea paralela a la línea de tierra que pase por el punto B0. La intersección de esta línea con r2 es la proyección vertical de B2 sobre r2.
Para determinar la proyección horizontal del punto B sobre r1, trazamos una línea perpendicular a la línea de tierra que pase por el punto B2. La intersección de esta línea con r1 es la proyección horizontal de B1 sobre r1.

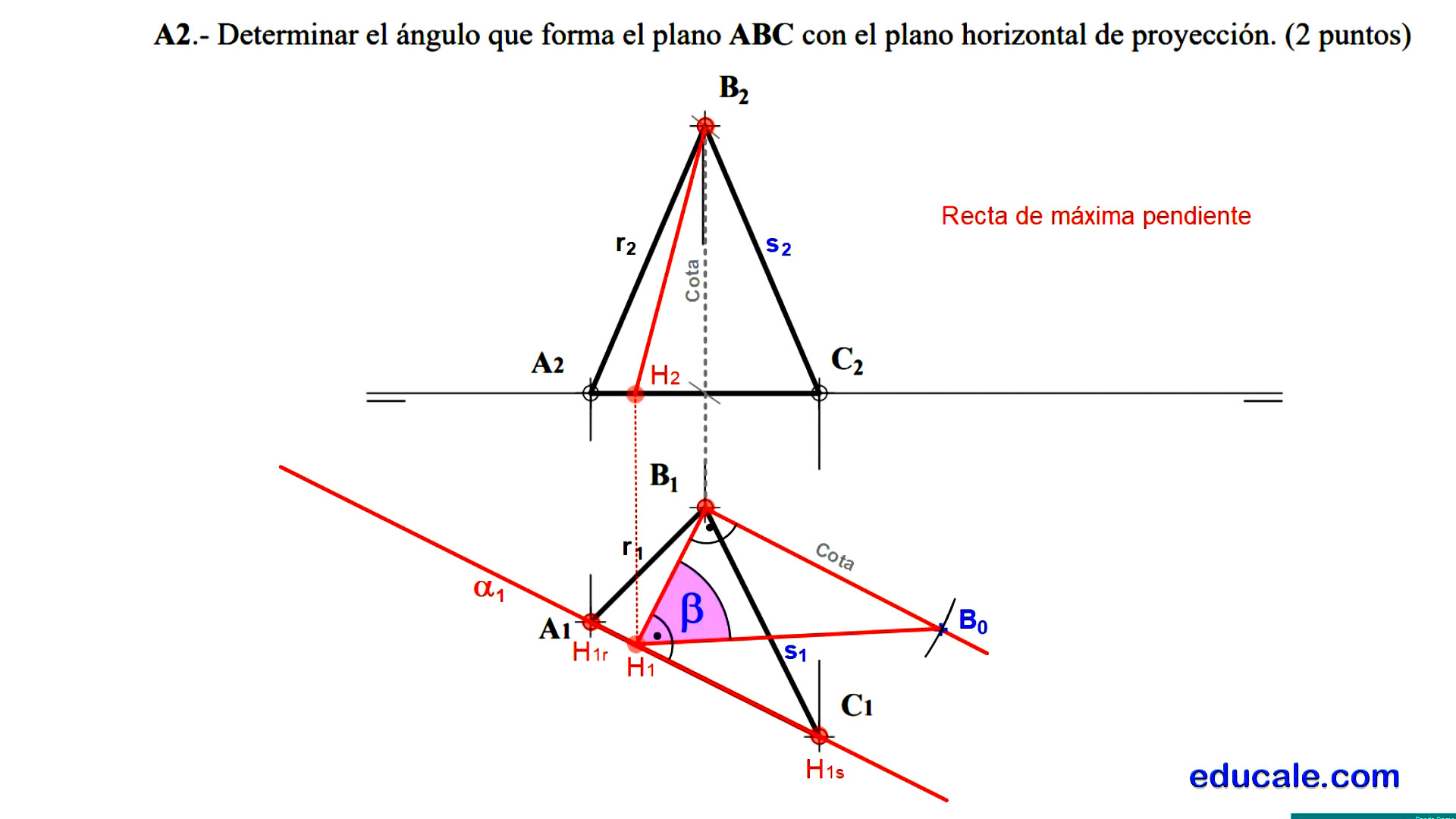
10.3 - Hallar el ángulo del plano con el plano horizontal de proyección

1.er método:
Abatimiento de la recta de máxima pendiente sobre un plano paralelo al plano vertical de proyección.
Se forma un triángulo rectángulo donde un cateto es la cota del vértice B y el otro cateto es la distancia entre B1 y H1. Esta distancia se lleva con el compás sobre la línea de tierra para determinar la posición de H0. Uniendo H0 con B2 se obtiene la hipotenusa del triángulo rectángulo. El ángulo agudo de H0 es el ángulo que forma el plano con el plano horizontal de proyección.
2º método:
Abatimiento de la recta de máxima pendiente sobre el plano horizontal de proyección.
Se forma un triángulo rectángulo donde un cateto es la cota del vértice B y el otro cateto es la distancia entre B1 y H1.
La cota del vértice B se lleva con el compás perpendicularmente al segmento B1, H1, obteniendo el vértice B abatido sobre el plano horizontal de proyección.
Uniendo B0 con H1 se obtiene la hipotenusa del triángulo rectángulo. El ángulo agudo de H1 es el ángulo que forma el plano con el plano horizontal de proyección.

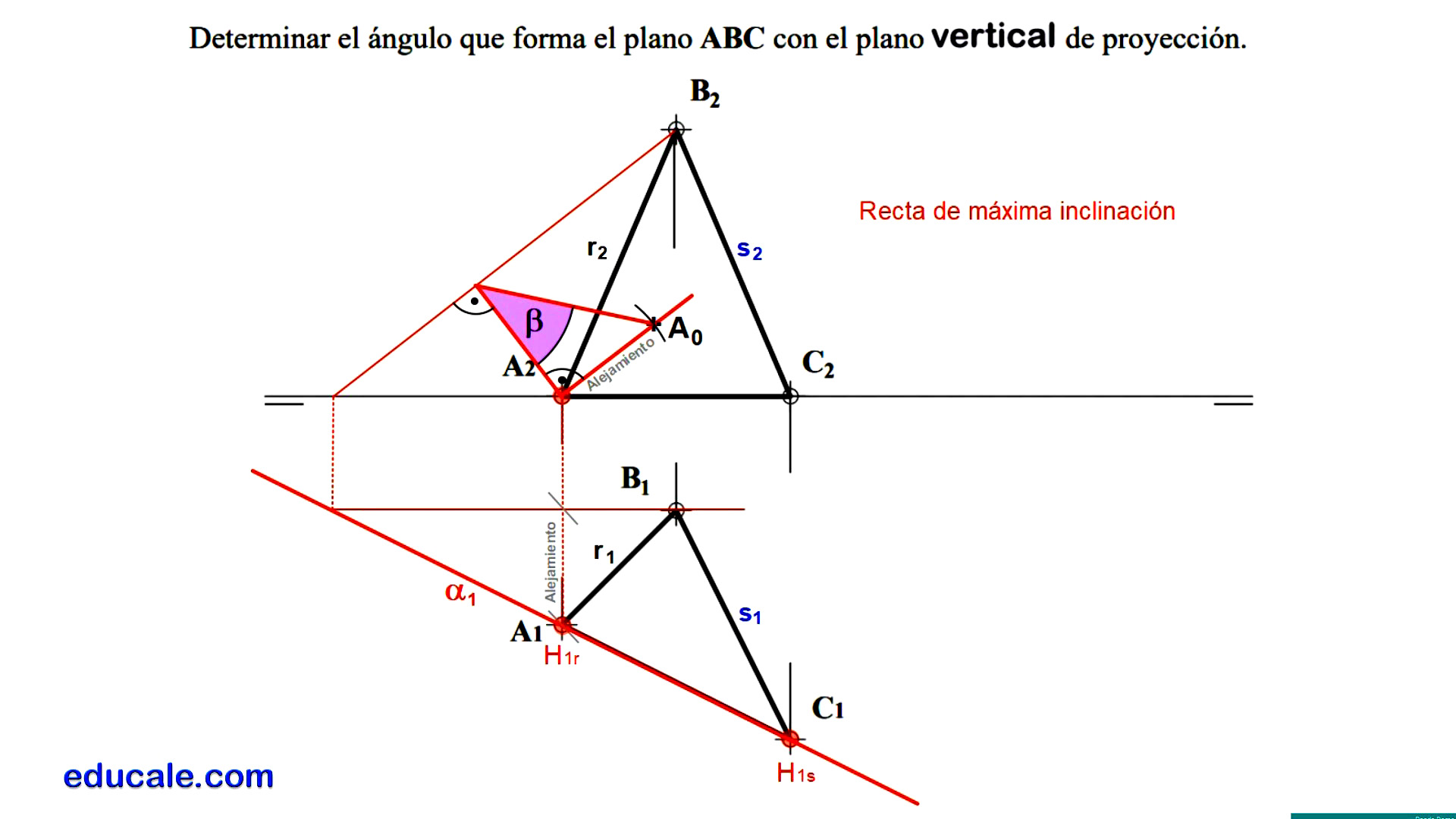
10.4 - Determinar el ángulo que forma el plano con el plano vertical de proyección

Hallamos las trazas horizontales de dos rectas.
Unido estas trazas dibujamos la traza horizontal del plano que las contiene.
En este caso la traza horizontal del plano coincide con la proyección horizontal del segmento AC.
Primer procedimiento:
Hallamos la recta frontal del plano que contiene el punto B.
Como el ángulo que nos piden es el formado con el plano vertical de proyección, tendremos que abatir la recta de máxima inclinación del plano.
Dibujaremos un triángulo rectángulo, donde un cateto será perpendicular a la proyección vertical de la recta frontal por A2 y el otro cateto será el alejamiento de A hasta la proyección horizontal de la recta frontal. Determinando el punto A abatido sobre un plano paralelo al plano vertical de proyección.
El ángulo que forma el plano con el plano vertical de proyección será el ángulo agudo del triángulo opuesto al vértice A0.
Segundo procedimiento:
En la última parte del video, se plantea un segundo procedimiento donde se determina la traza vertical del plano y se abate la recta de máxima pendiente que pasa por A2 sobre el plano vertical de proyección. Finalmente, se demuestra que este proceso es más complejo que el primero.

10.5 - Abatimiento de un plano cuyas trazas se cortan fuera del papel con la línea de tierra, mediante el nuevo método de abatimiento de planos oblicuos por medio del abatimiento de sus rectas

Las trazas del plano son oblicuas a la línea de tierra y no se cortan con ella dentro del papel. Debemos de utilizar el siguiente procedimiento nuevo.
Por los puntos A y B se hacen pasar dos rectas que corten a la línea de tierra y que sus trazas estén dentro del papel.
Abatimos sus trazas verticales, que posteriormente uniremos con sus trazas horizontales, formando triángulos rectángulos en los que sus hipotenusas serán la distancia real entre las trazas.

Abatiremos nuevamente las trazas verticales para obtener el plano abatido sobre el plano horizontal de proyección.
Desde las proyecciones horizontales de las trazas verticales se dibujan rectas perpendiculares a la traza alfa1.
Con centros en las trazas horizontales H1, y radios iguales a las distancias de las hipotenusas de los triángulos rectángulos, dibujaremos arcos que al cortasen con las anteriores perpendicular nos darán los puntos V abatidos sobre PH.
Uniendo estas trazas verticales abatidas, hallaremos la traza horizontal del plano abatido sobre el plano horizontal de proyección.

Sobre estas rectas abatidas hallamos los puntos A y B abatidos.
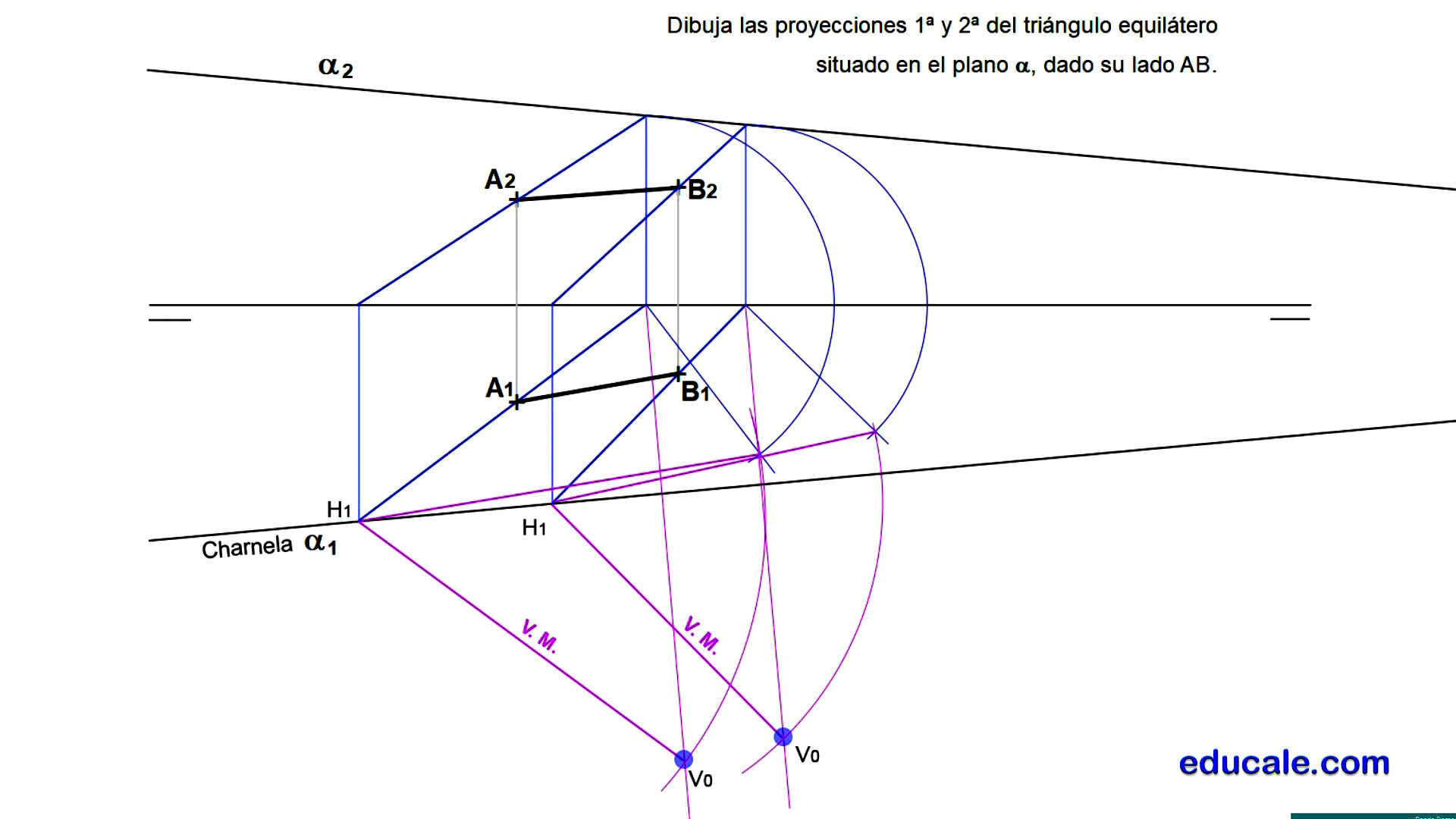
Dibujamos el triángulo equilátero requerido de lado AB, obtenido el vértice C0.
Localizamos C1 mediante homología afín.
Determinamos la traza horizontal de la recta AC.
Las proyecciones H2 y A2 se unen para formar un segmento en el que se encontrará la proyección vertical del punto C.