@educale EDUCALE.COM
4 – Dibujo de polígonos regulares dada la SUMA o DIFERENCIA
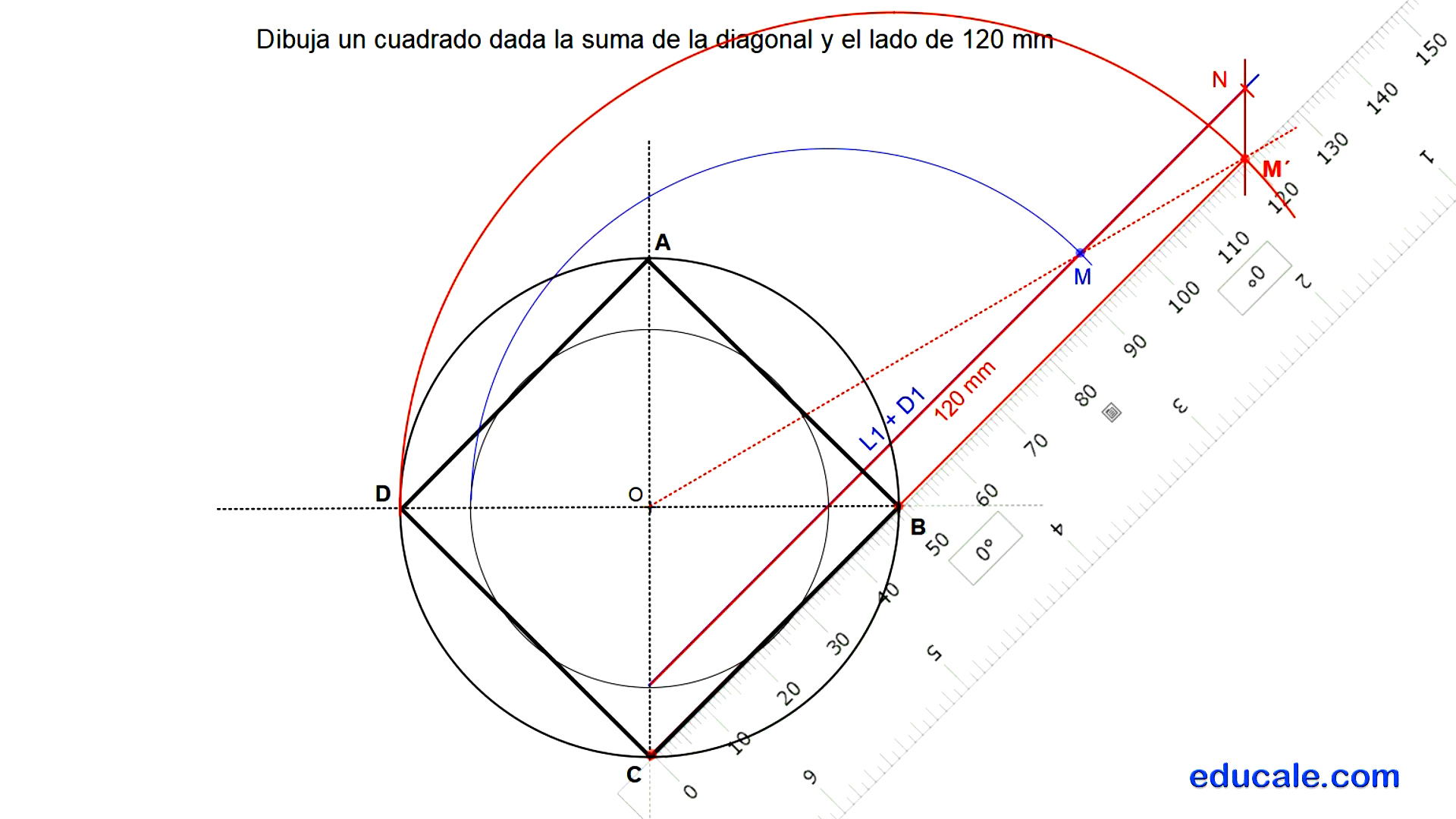
4.1 - Dibuja un cuadrado dada la SUMA de la diagonal y el lado.
Dibujamos un cuadrado cualquiera inscrito en una circunferencia.
Prolongamos uno de sus lados y sobre este se suma su diagonal o diámetro de la circunferencia.
Sobre el segmento L1+D1 se miden los 120 mm dados
.
Por el extremo N se traza una recta paralela al eje vertical AC, cortando a la recta OM en el punto homologo M´.
Dibujamos una recta paralela a L1+D1 por M´.
Esta recta paralela cortará a los ejes de simetría en los vértices B y C solución.
Con centro O, que es el centro de homología, y radio hasta B se dibuja una circunferencia para hallar los otros dos vértices A y D.
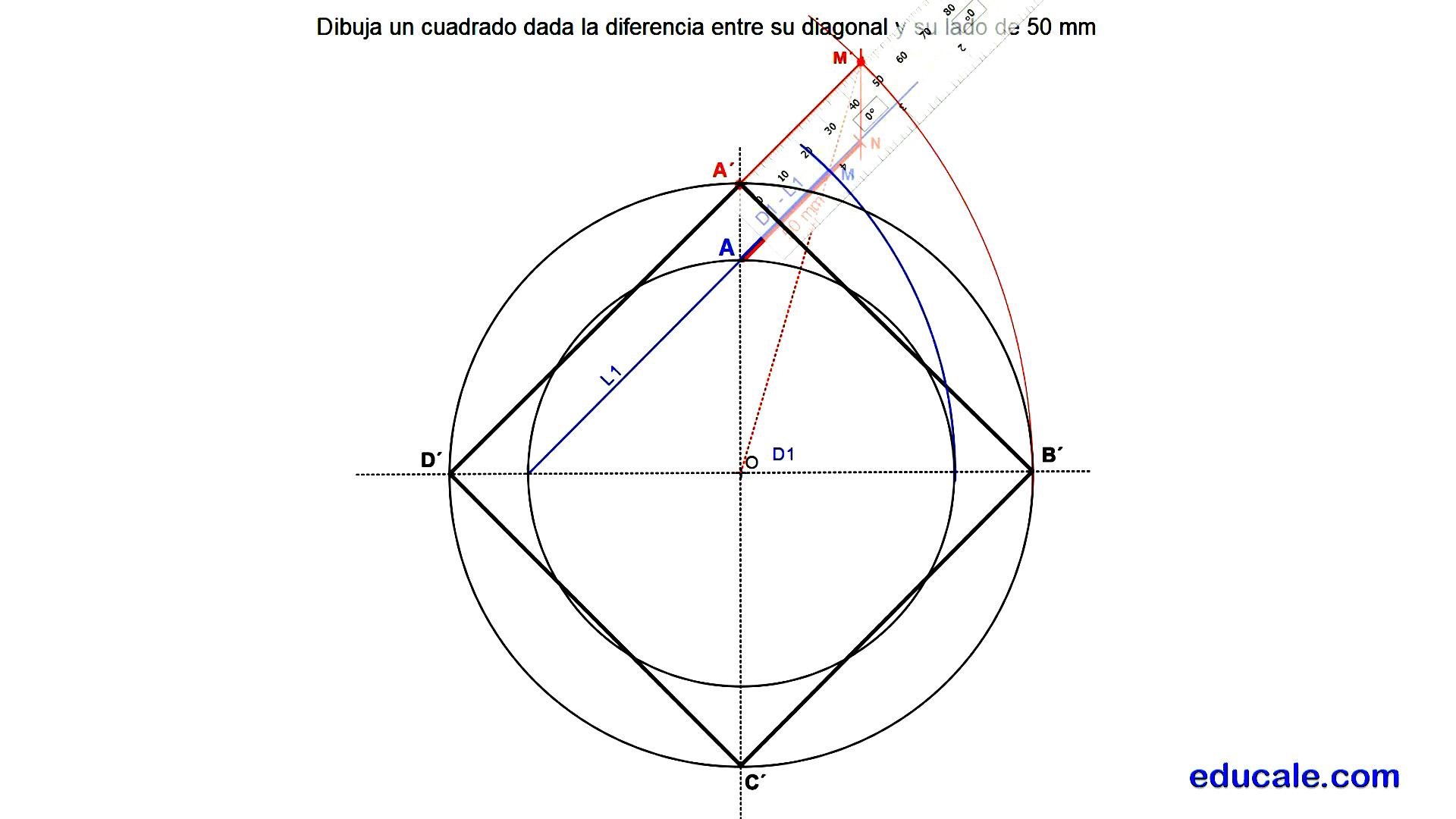
4.2 - Dibuja un cuadrado dada la DIFERENCIA entre su diagonal y su lado.
Dibujamos un cuadrado cualquiera inscrito en una circunferencia.
Prolongamos uno de sus lados y con centro en el vértice exterior se realiza la diferencia de su diagonal menos su lado AM.
Sobre el segmento se miden los 50 mm dados.
Por el extremo N se dibuja una recta paralela al eje vertical, cortando a la recta OM en el punto homologo M´.
Dibujamos una recta paralela a L1 por M´.
Esta recta paralela cortará a los ejes de simetría en los vértices A´ y D´ solución.
Con centro O, que es el centro de homología, y radio hasta A´ se dibuja una circunferencia para hallar los otros dos vértices B´ y C´.
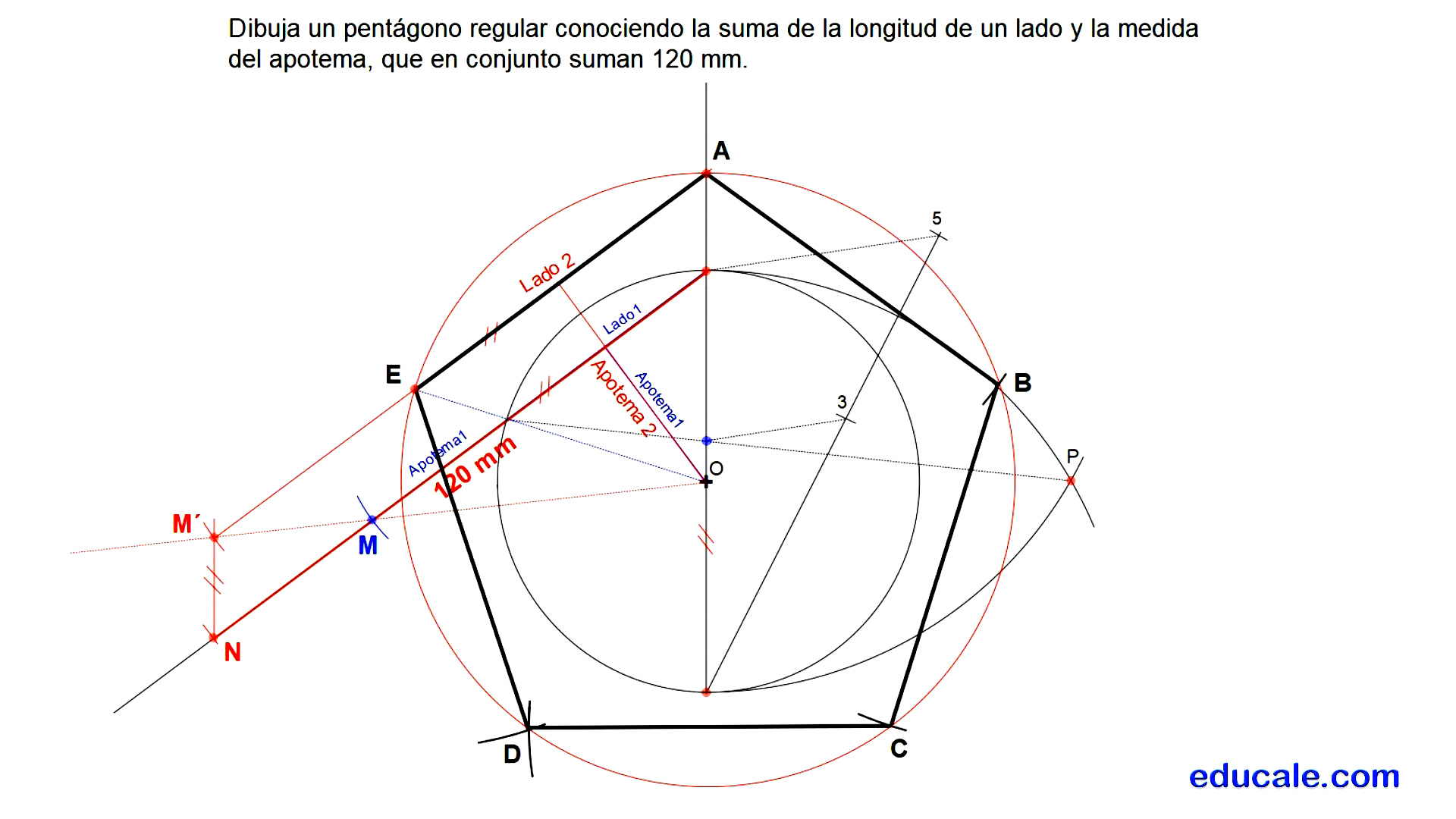
4.3 - Dibuja un pentágono regular conociendo la SUMA de su lado y su apotema.
1.- Hallamos el lado un pentágono cualquiera inscrito en una circunferencia.
Dibujamos una circunferencia con centro en un punto cualquiera de esta.
Dividimos su diámetro en cinco partes iguales, pero solo marcamos la tercera parte.
Localizamos el medidor P trazando arcos con un radio igual al diámetro.
Se une P con esta parte del diámetro para hallar la longitud del lado del pentágono.
2.- Por el centro de homotecia O se dibuja una perpendicular a este lado para hallar su apotema.
3.- Al lado L1 se le suma su apotema. Sobre este segmento se sitúa la suma dada de 120 mm.
4.- Hallar el radio de la circunferencia solución.
Por el extremo N se dibuja una recta paralela al eje vertical, cortando a la recta OM en el punto homologo M´.
Dibujamos una recta paralela a L1 por M´.
Esta recta paralela cortará al eje de simetría en el vértice A solución.
Con centro O, que es el centro de homología, y radio hasta el vértice A se dibuja una circunferencia para hallar los otros vértices.
5.- El centro de homología O se une con el otro extremo de L1 para hallar la longitud del lado solución L2.
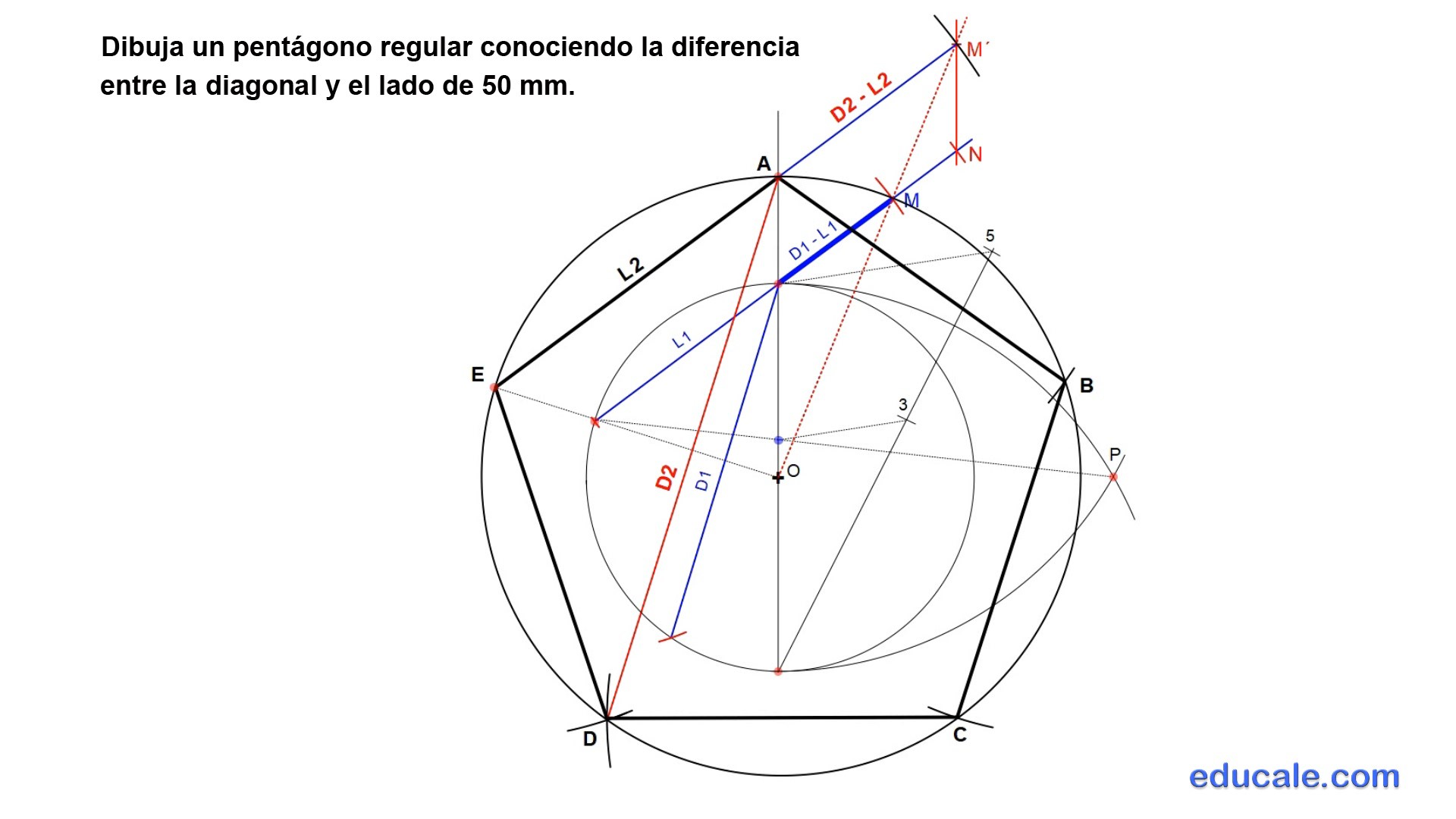
4.4 - Dibuja un pentágono regular conociendo la DIFERENCIA entre la diagonal y el lado de 50 mm.
1.- Hallamos el lado un pentágono cualquiera inscrito en una circunferencia.
Dibujamos una circunferencia con centro en un punto cualquiera de esta.
Dividimos su diámetro en cinco partes iguales, pero solo marcamos la tercera parte.
Localizamos el medidor P trazando arcos con un radio igual al diámetro.
Se une P con esta parte del diámetro para hallar la longitud del lado del pentágono.
2.- con el compás trasladamos este lado para hallar la longitud de su diagonal D1.
3.- Al lado L1 y desde su extremo exterior se realiza la diferencia D1 – L1. Sobre este segmento se sitúa la diferencia dada de 50 mm.
4.- Hallar el radio de la circunferencia solución.
Por el extremo N se dibuja una recta paralela al eje vertical, cortando a la recta OM en el punto homologo M´.
Dibujamos una recta paralela a L1 por M´.
Esta recta paralela cortará al eje de simetría en el vértice A solución.
Con centro O, que es el centro de homología, y radio hasta el vértice A se dibuja una circunferencia para hallar los otros vértices.
5.- El centro de homología O se une con el otro extremo de L1 para hallar la longitud del lado solución L2.