@educale EDUCALE.COM
2 – Dibujo de polígonos regulares dada la DIAGONAL
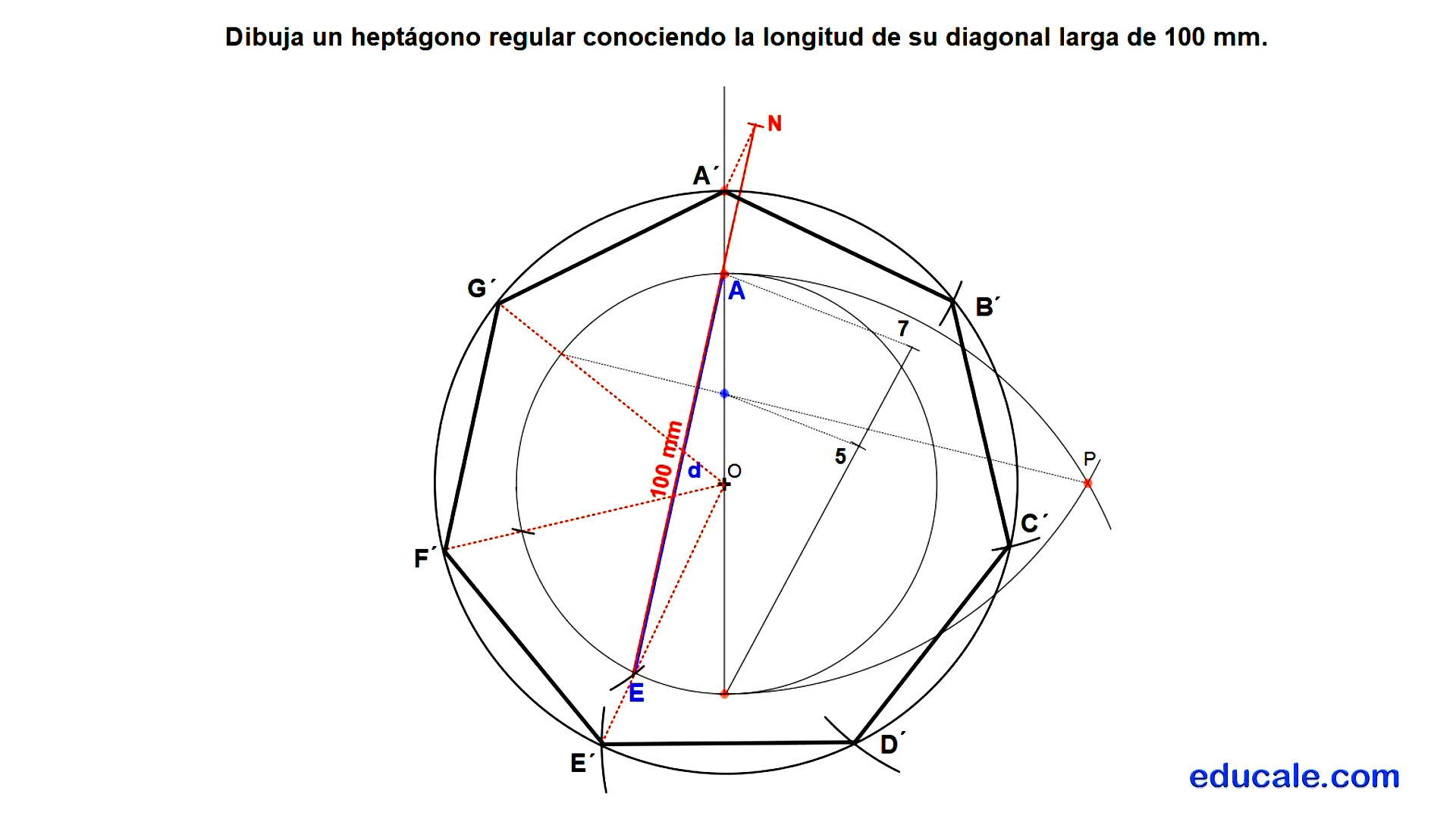
3.1 - Dibuja un heptágono regular conociendo la longitud de su diagonal larga de 100 mm.
1.- Se dibuja la mitad de un heptágono cualquiera.
Dividimos su diámetro en siete partes iguales, pero solo marcamos la parte quinta.
Localizamos el medidor P trazando arcos con un radio igual al diámetro.
Se une P con esta parte del diámetro para hallar la longitud del lado del heptágono.
Con el compás trasladamos la medida del lado para hallar el vértice E.
Se unen estas partes con el centro de homotecia O.
2.- Ampliación o reducción de la diagonal.
El segmento AE será su diagonal larga. Sobre esta y a partir de E, se mide la longitud dada de 100.
Por el otro extremo M se dibuja una recta paralela al segmento OE, cortando al diámetro en el vértice solución A´.
Con radio OA´ se dibuja la circunferencia buscada.
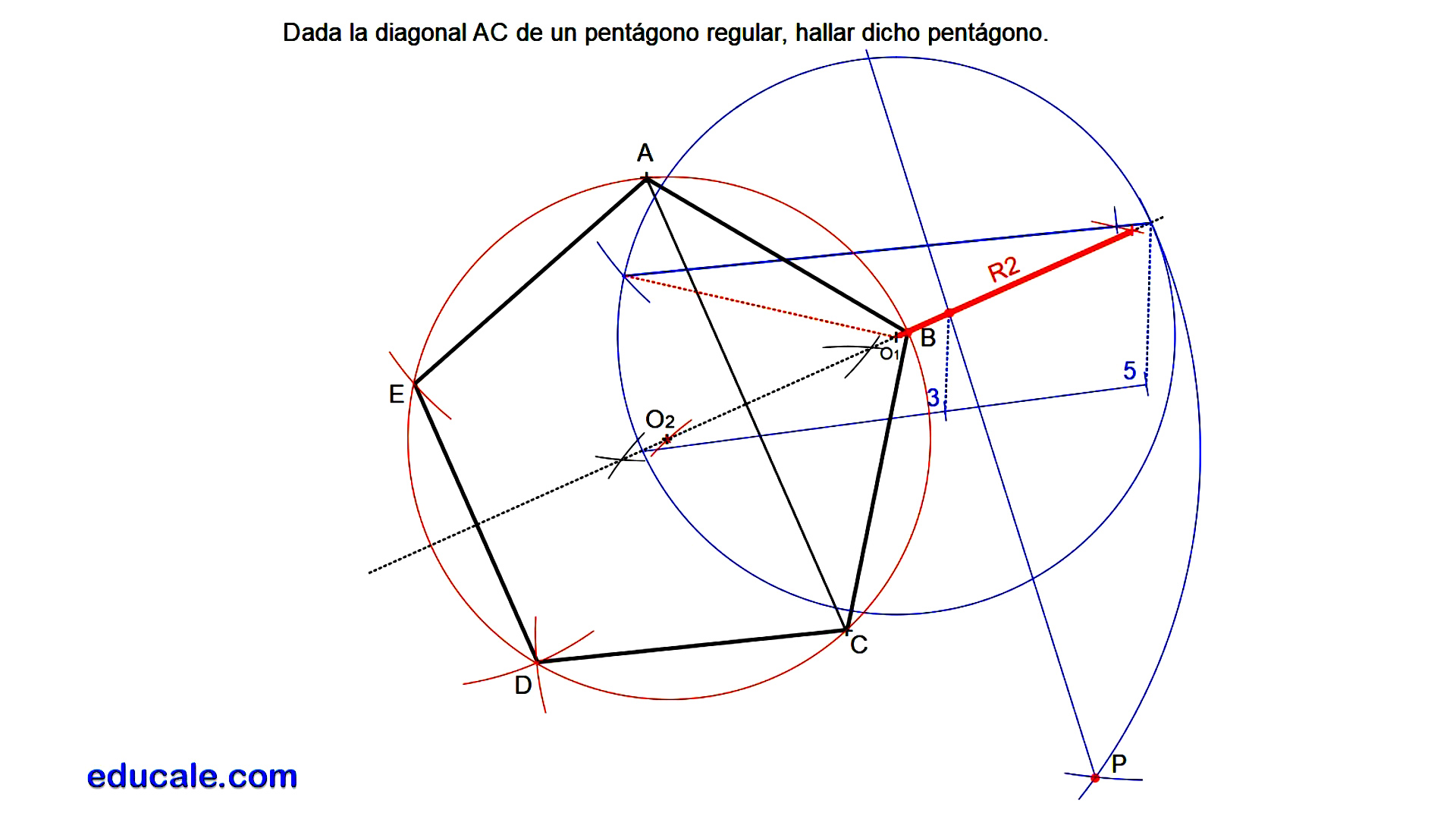
3.2 - Dada la diagonal AC de un pentágono regular, hallar dicho pentágono.
Trazamos la mediatriz de la diagonal dada.
Dibujamos una circunferencia con centro en un punto cualquiera de esta.
Dividimos su diámetro en cinco partes iguales, pero solo marcamos la tercera parte.
Localizamos el medidor P trazando arcos con un radio igual al diámetro.
Se une P con esta parte del diámetro para hallar la longitud del lado del pentágono.
Con el compás trasladamos la medida del lado para hallar su diagonal.
Trasladamos la medida de la diagonal dada sobre esta otra a partir de un vértice.
Por el otro extremo se dibuja una paralela al segmento del vértice, a partir de donde medimos la diagonal, con el centro, hallando la longitud del radio de la circunferencia buscada.
Con centro en A se traslada este radio para hallar el centro de la circunferencia solución.
El dibujo de esta circunferencia nos determinará el vértice B.
Con la longitud del lado AB se hallan los vértices E y D.
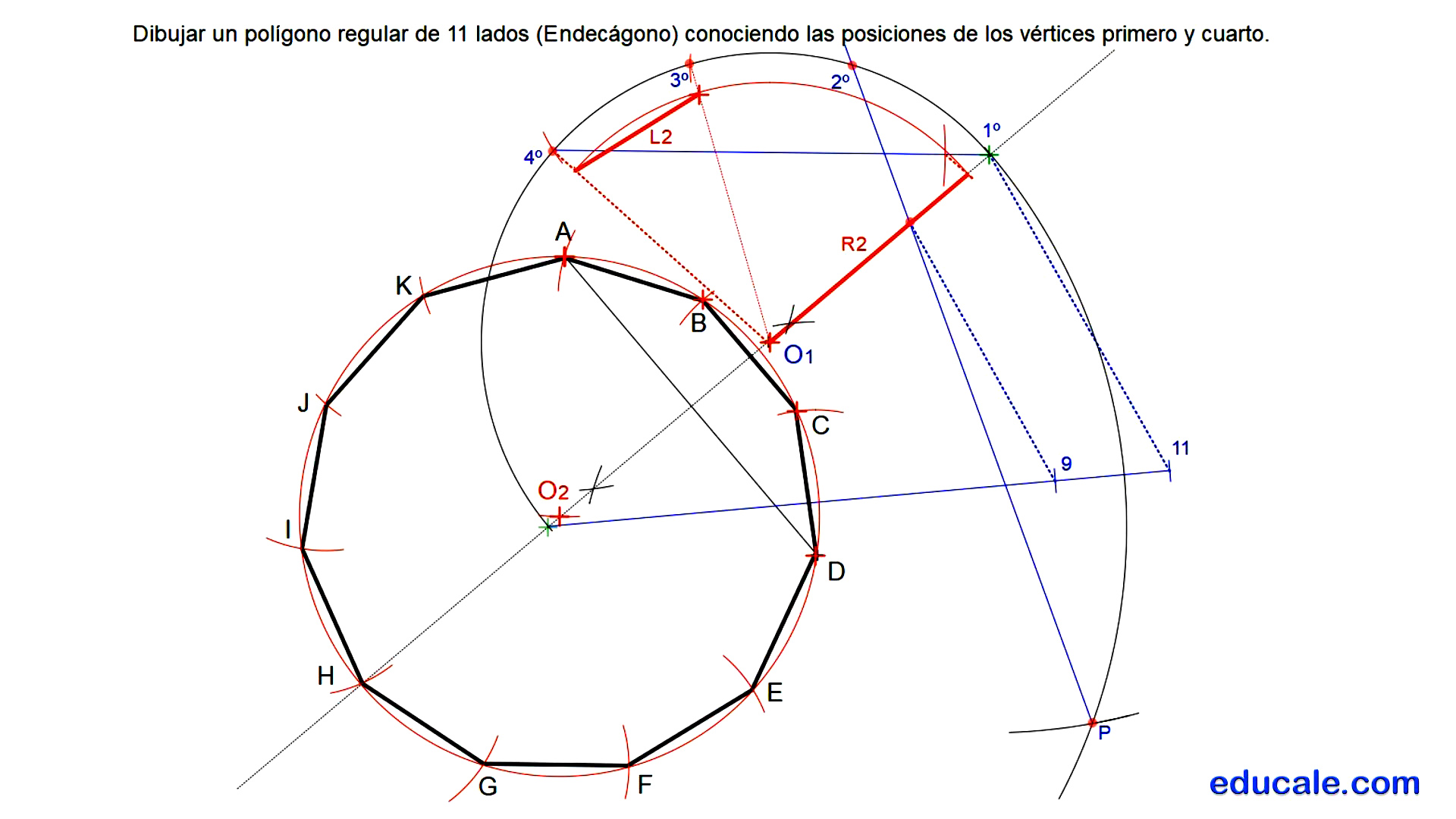
3.3 - Dibujar un polígono regular de 11 lados conociendo las posiciones de los vértices primero y cuarto.
Trazamos la mediatriz de la diagonal dada.
Dibujamos una circunferencia con centro en un punto cualquiera de esta.
Dividimos su diámetro en once partes iguales, pero solo marcamos la novena parte.
Localizamos el medidor P trazando arcos con un radio igual al diámetro.
Se une P con esta parte del diámetro para hallar la longitud del lado del endecágono.
Con el compás trasladamos la medida del lado para hallar su diagonal.
Trasladamos la medida de la diagonal dada sobre esta otra a partir de un vértice.
Por el otro extremo se dibuja una paralela al segmento del vértice, a partir de donde medimos la diagonal, con el centro (O1), hallando la longitud del radio de la circunferencia buscada.
Con centro en O1 dibujamos un arco con este radio para hallar la longitud del lado buscado.
Con centro en A se traslada este radio para hallar el centro de la circunferencia solución.
Con la longitud del lado 2 se hallan los vértices del endecágono.