1º Se elige un punto C cualquiera, no alineado con los otros.
2º Mediante mediatrices (el Circuncentro), se traza la circunferencia que pase por A, A´y C.
3º Hallamos C´, el inverso de C.
4º Dibujamos la circunferencia que pase por C, C´ y B, para hallar B´, el inverso de B..

La INVERSIÓN
La Inversión es una transformación geométrica en la que a una figura corresponde otra y en la que se cumple que:

Dos puntos inversos (A, A’) están alineados con un punto fijo llamado Centro de Inversión (O),
El producto de la distancia de un punto al Centro de Inversión por la distancia de su inverso al Centro de Inversión es constante (K) y se llama Potencia de Inversión.
Esto quiere decir que OA·OA’ = OB·OB’ = OT·OT = K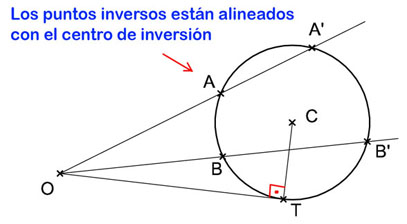

Trazando sucesivas rectas secantes a esta circunferencia encontramos más puntos y sus inversos. Puesto que K es constante, cuanto mayor sea OA, menor será OA’, es decir, cuando más alejado esté un punto A del Centro O, más cerca estará su inverso A’ del Centro O.

Existe una distancia para la cual un punto A y su inverso son iguales.
Lo puedes ver en el dibujo anterior. Se trata del punto de tangencia. El punto T coincide con su inverso y para él también se cumple que
OT·OT = K
Por tanto,
OT = Raíz cuadrada de K