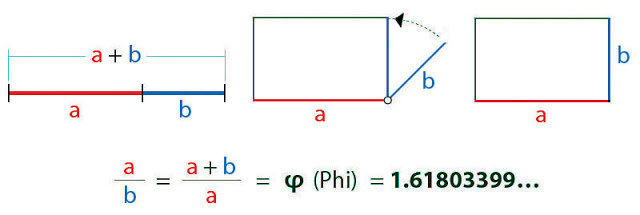
La proporción áurea de un segmento "a" dado es otro segmento "b", fruto de su división, de tal manera que la relación entre el segmento mayor "a"dado y el mediano resultante de la división "b", sea la misma que la relación entre el mediano "b" el pequeño resultante "c". (El pequeño es al mediano lo mismo que el mediano al mayor).

a/b=b/c; c/b=b/a

El segmento mediano "b" es por tanto es media proporcional entre el grande "a" y el pequeño "c".
Cuando se da esta situación, la razón de proporcionalidad es siempre constante e igual a µ, siendo µ el número áureo y de valor 1,618. La división del segmento dado que hace posible esta relación se denomina Sección Áurea.

µ=b/c= 1,618

Trazado de la Proporción Áurea

Dado un segmento de 100 mm. se dibuja una perpendicular en un extremo, midiendo la mitad del segmento dado.
Unimos los dos extremos, formando un triángulo rectángulo.
Con centro en C trazamos un arco de radio CB, hasta cortar a la prolongación en E.
El segmento AE será la división áurea de AB.

Rectángulo áureo
Es aquel que tiene la relación áurea (1.618) de cociente entre su lado mayor y menor.
Para construir un rectángulo áureo de base "a" dada, tomaremos como altura su división áurea "b" obtenida.

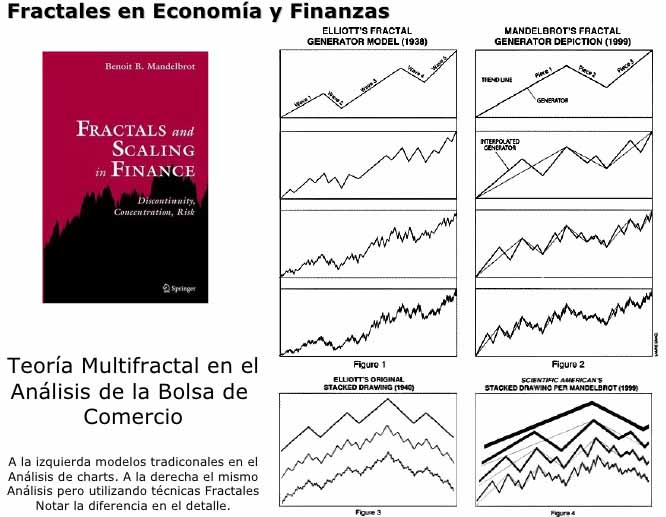
Aplicaciones de la proporción ÁUREA
El número áureo (también llamado número de oro, razón extrema y media, razón áurea, razón dorada, media áurea, proporción áurea y divina proporción) es un número irracional, representado por la letra griega φ (phi) (en minúscula) o Φ (Phi) (en mayúscula).
Se le atribuye un carácter estético a los objetos cuyas medidas guardan la proporción áurea. A lo largo de la historia, se ha atribuido su inclusión en el diseño de diversas obras de arquitectura y otras artes. Predomina en toda la naturaleza.
El Hombre de Vitruvio o Estudio de las proporciones ideales del cuerpo humano es un famoso dibujo acompañado de notas anatómicas de Leonardo da Vinci.

La serie de Fibonacci es una sucesión infinita de números naturales: 0, 1, 1, 2, 3, 5, 8, 13, 21,… Los dos primeros números de la sucesión son 0 y 1. Los otros términos son la suma de los 2 términos anteriores en la sucesión: 0+1=1, 1+1=2, 1+2=3, 2+3=5, 3+5=8, 5+8=13…

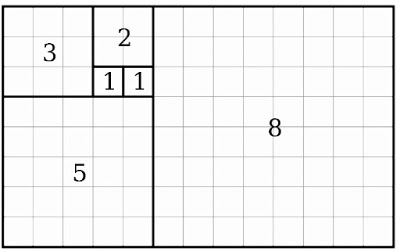
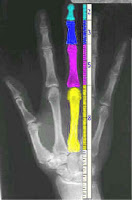
El descubrimiento de Fibonacci nos entrega otras sorpresas como su aplicación en diferentes áreas, como en la imagen que se encuentra a continuación donde se construye un rectángulo con cuadrados internos que son la longitud de los números Fibonacci. Este rectángulo se asemeja al rectángulo áureo.
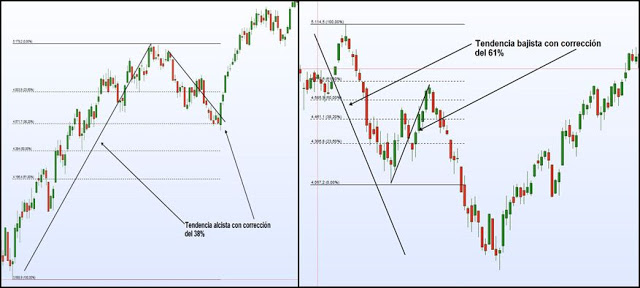
Podemos medir los niveles correctivos de los graficos de bolsa por Fibonacci y buscar posible paradas en niveles de 38% de 50% o de 61,8%... relacionandose con la onda o diente de sierra anterior. funciona en graficos semanales, diarios, horas, minutos... Estos gráficos bursátiles guardan una estrecha relación con los fractales.